Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 20
No exercício a seguir, o gráfico da equação é uma elipse ou uma hipérbole. Ache o centro, vértices e focos da cônica. Se o gráfico for uma elipse, ache também as extremidades do eixo menor. Se o gráfico for uma hipérbole, ache também as equações das assíntotas. Faça um esboço da curva e mostre os focos. Se a curva for uma hipérbole, trace também as assíntotas.
Passo 1
Bom, primeiro que a gente não sabe se isso é uma hipérbole ou uma elipse. Então vamo lá tentar descobrir? SIMBORA!
Para fazer tal coisa, a gente deve primeiro pegar essa equação e deixar ela na forma reduzida, pra gente trabalhar com a parte fácil do negócio! Então, vamos ajeitar isso daí.
Bem, chegando aqui a gente agora vai aplicar a técnica de completar o quadrado. A gente observa que se parecem com dois termos elevados ao quadrado, faltando só uma parte. Então a gente pode reescrever eles de uma forma mais simples, subtraindo o que está faltando. Belezinha? Então vamo continuar:
AEEEE!! Conseguimos chegar na nossa tão sonhada EQUAÇÃO REDUZIDA! E a gente já pode dizer que isso é uma hipérbole, pois entre os termos de “x” e “y”, há uma subtração.
Outro ponto a se observar aqui, é que essa hipérbole corresponde a um caso de translação, ou seja, ela não está centrada na origem. Mas calma, isso é facilmente corrigido.
Passo 2
Então já que chegamos na nossa hipérbole, vamos procurar o que a gente quer dela!
Antes de mais nada, devemos lembrar que nessa equação, o “x” e o “y” da equação não estão sozinhos (estão sendo somados/subtraídos de algum valor), logo, a nossa hipérbole não está centrada na origem. Então o primeiro passo é transformar as nossas coordenadas xy em coordenadas x’y’. E é bem fácil, relaxa 😊
Sim, está feito. E não, não é zoeira kkkkkk. Já que a gente considerou agora (depois da transformação) que o centro está na origem, vamos definir o que é cada coisa aqui.
Logo:
E também:
E da fórmula:
Ja temos o nescessário para acharmos os Focos e os Vértices da nossa hipérbole. Nos vértices e nos focos, a gente vai considerar A’, B’ e F’ (já que estamos nas coordenadas x’y’).
Então agora vamos atrás das assíntotas, e relaxem, é mamão com açúcar (bebam água e comam frutas, sem açúcar de preferência kkkkk). Elas obedecem a seguinte regra (para casos em que ela está com os focos no eixo x):
Facinho né galera? Então vambora!
Passo 3
Ufa, tamo quase terminando!! Agora pra matar a questão de vez, a gente vai voltar ao sistemas de coordenadas xy. Pra isso, vamos fazer a seguinte:
Lembra que a gente antes fez essas transformações?
Agora vamos desfazer, pra termos a resposta do jeito que deve ser!! Para fazer isso, vamos pegar os pares ordenados de cada elemento que a gente achou lá em cima, e substituir pelas equações... Não entendeu? Relaxa! Vamos para a prática:
Temos que:
Substituindo em A’, para o x:
E para o y:
Logo:
Entenderam? Facinho facinho. Agora vamos para o resto dos vértices e focos, usando a mesma regra 😊
Agora para o F:
E agora pra matar a questão, vamos para o esboço:
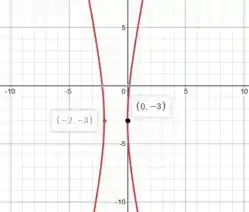
Resposta
Assíntota: