Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.Exercícios práticos - Ex. 86
A região “triangular” no primeiro quadrante delimitado pelo eixo , a reta e a hipérbole é girada em relação ao eixo para gerar um sólido. Encontre o volume do sólido.
Passo 1
Olá galerinha, tudo bem com vocês? Vem comigo que vamos resolver este exercício juntos!
Primeiramente iremos relembrar algumas definições. Uma hipérbole é o conjunto de pontos em um plano cujas distâncias a partir de dois pontos fixos nesse plano têm uma diferença constante. Os dois pontos fixos são os focos da hipérbole.
A reta que passa pelos focos de uma hipérbole é o eixo focal. O ponto no eixo na metade do trajeto entre os focos é o centro da hipérbole. Os pontos onde o eixo focal e a hipérbole se cruzam são os vértices, isso é explicado pela seguinte Figura:
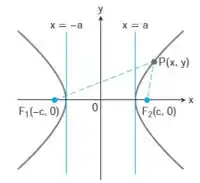
A equação da forma padrão para hipérbole centradas na origem:
Além disso, a equação do volume do sólido é dada por:
Então vamos lá! Pelo enunciado, temos a seguinte equação:
Para deixarmos no formato padrão de uma elipse, iremos dividir ambos os lados por 36:
Onde:
Se utilizarmos o programa computacional para obtermos nossas duas curvas dada no enunciado, conseguimos obter o seguinte:
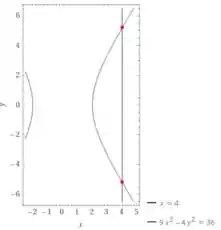
Passo 2
De acordo com o enunciado, queremos essa função “triangular”:
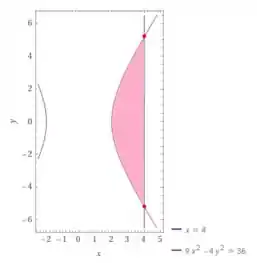
Para esta região, queremos o volume quando é girada em torno do eixo . Sendo assim, iremos isolar em função de :
Ou seja:
Para a região delimitada, o valor de inicial é o valor de e o final da reta , sendo assim temos:
Resposta
.