Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.3 - Ex. 26
(a) Encontre uma equação da reta tangente à curva no ponto .
(b) Ilustre a parte (a) fazendo o gráfico da curva e da tangente na mesma tela.
Passo 1
Fala aí! tudo certinho?
Nesse problema fio dada a função
E nosso objetivo é determinar a equação da reta tangente a essa função no ponto e esboçar e a reta.
Parece complicado?
Primeiramente vamos relembrar como calculamos uma reta tangente a uma curva?
A equação que descreve uma reta é dada por
No caso de uma reta tangente, podemos dizer que , ou seja, a derivada de aplicada no ponto e é o ponto de tangencia da curva.
Bora lá!
Passo 2
Pelos dados do enunciado, temos que . Então só nos resta derivar e aplicar o ponto .
Se , derivando essa curva, vamos obter
Pela regra da potência, sabemos que
E pelo teorema fundamental do cálculo, a derivada de é
Substituindo em , vamos obter
Aplicando o ponto , temos
Tranquilo até aqui?
Passo 3
Como vimos no passo 1, e é o ponto de tangencia da curva.
Substituindo essas informações na equação da reta, vamos obter que
Simplificando essa expressão, vamos obter
Show?
Passo 4
Por fim, temos que esboçar os gráficos da curva e da reta tangente...
A reta tangente é mais fácil, se então a reta vai cruzar o eixo em e o eixo em .
Já a função dada no problema tem um termo linear que é somado à função trigonométrica . Assim essa função pode ser expressa como a reta com uma oscilação devido à soma com .
Condensando tudo isso em um gráfico, vamos obter
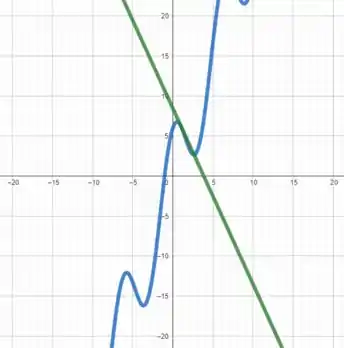
É isso! O que achou? Responde Aí!