Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.2 - Ex. 35

Encontre uma equação para a reta que é tangente à curva y = x 3 - 2 x + 1 no ponto 0,1 e use um recurso gráfico para fazer, na mesma tela, os gráficos da curva e de sua tangente.

Passo 1

Primeiros vamos usar a Definição 2.2 . 1 para encontrar a derivada em x = 0 :

f ' x = lim h → 0 ⁡ f x + h - f x h

Vamos então aplicar:

f ' 0 = lim h → 0 ⁡ f 0 + h - f 0 h = lim h → 0 ⁡ 0 + h 3 - 2 0 + h + 1   - 0 3 - 2 ⋅ 0 + 1   h

Agora vamos manipular o limite:

lim h → 0 ⁡ 0 + h 3 - 2 0 + h + 1   - 0 3 - 2 ⋅ 0 + 1   h = lim h → 0 ⁡ h 3 - 2 h + 1   - 1   h =

= lim h → 0 ⁡ h 3 - 2 h + 1   - 1 h = lim h → 0 ⁡ h 3 - 2 h h

E por último vamos cancelar o termo h do numerador e do denominador e vamos aplicar o limite:

lim h → 0 ⁡ h 3 - 2 h h = lim h → 0 ⁡ h 2 - 2 = 0 2 - 2 = - 2

Passo 2

Agora vamos encontrar a reta tangente ao gráfico de y = f x em x = 0 .

A equação da reta tangente é do seguinte formato:

y - f x 0 = f ' x 0 x - x 0

Onde x 0 , y 0 é o ponto da reta tangente à curva e f ' x 0 é a inclinação da reta tangente.

Passo 3

Pronto, temos todas as informações, vamos então substituir os valores na equação, o ponto 0 , 1 e a inclinação f ' 0 = - 2 :

y - f x 0 = f ' x 0 x - x 0 →

y - 1 = - 2 x - 0 →

y - 1 = - 2 x →

y = - 2 x + 1

Passo 4

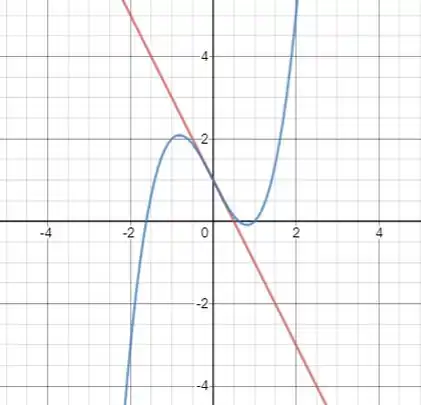
Agora temos o gráfico da curva, em azul, e de sua tangente, em vermelho:

Resposta

y = - 2 x + 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercícios de 1 a 20, faça o seguinte: (a) Trace um esboço do gráfico da função; (b) determine se f é contínua em x 1 ; (c) calcule f ´ _ _ ( x 1 ) e f ´ + x 1 , se existirem, (d) determine se f é
Nos exercícios de 1 a 20, faça o seguinte: (a) Trace um esboço do gráfico da função; (b) determine se f é contínua em x 1 ; (c) calcule f ´ _ _ ( x 1 ) e f ´ + x 1 , se existirem, (d) determine se f é
Nos exercícios de 1 a 20, faça o seguinte: (a) Trace um esboço do gráfico da função; (b) determine se f é contínua em x 1 ; (c) calcule f ´ _ _ ( x 1 ) e f ´ + x 1 , se existirem, (d) determine se f é
Nos exercícios de 1 a 20, faça o seguinte: (a) Trace um esboço do gráfico da função; (b) determine se f é contínua em x 1 ; (c) calcule f ´ _ _ ( x 1 ) e f ´ + x 1 , se existirem, (d) determine se f é