Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.2 - Ex. 6a
Nos exercícios de 1 a 20, faça o seguinte: (a) Trace um esboço do gráfico da função; (b) determine se é contínua em ; (c) calcule e se existirem, (d) determine se é derivável em .
6.
Passo 1
Letra (a)
O esboço do gráfico da função pode ser obtido utilizando o programa de computador Geogebra. Assim, o esboço do gráfico da função é:
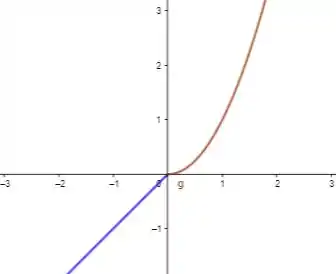
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
43. a) Use uma calculadora para tabular até quatro casas decimais, valores de s e n π 3 + h - s e n π 3 h Quando hé1 ;0,5 ;0,1 ;0,01 ;0,001 ;ehé- 1 ;- 0,5 ;- 0,1 ;- 0,01 ;- 0,001 é é . A que o quocien
44. b) Ache lim h → 0 c o s 5 π 6 + h - c o s 5 π 6 h , Interpretando-o como uma derivada.
46. b) Ache lim h → 0 sec π 6 + h - sec π 6 h Interpretando-o como uma derivada.
54. Se f e g são duas funções, tais que suas derivadas primeira e segunda existem e h é uma função definida pela equação hx =f x ⋅ g ( x ) , prove que h ' ' ( x ) = f x ⋅ g ' ' x+2 f ' x g ' x +f ' '
56. Se y = 1 1 - 2 x Prove, por indução matemática, que d n y d x n = 2 n n ! 1 - 2 x n + 1