Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.2 - Ex. 24
Seja . Use um argumento geométrico para encontrar .
Passo 1
Primeiro vamos analisar geometricamente, temos que é metade de um círculo.
Agora vamos achar para analisar o ponto:
Passo 2
Vamos agora analisar a reta tangente no ponto vendo o gráfico abaixo:
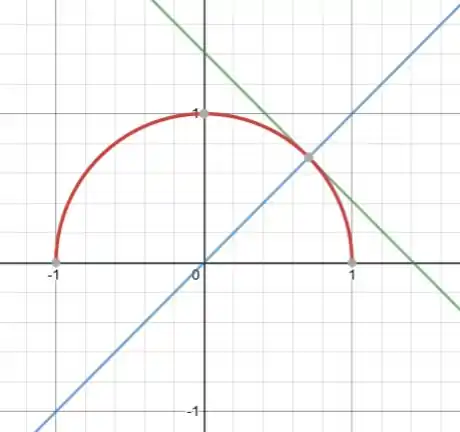
Pelo gráfico vemos que a reta tangente, de verde, é perpendicular à reta , de azul, e dessa reta temos que a inclinação, que é o coeficiente ligado à , é:
Passo 3
E agora por último sabemos que podemos achar a inclinação de uma reta que é perpendicular à outra da forma:
Vamos então aplica, temos que a inclinação no ponto é a derivada nesse ponto, assim:
Resposta
Exercícios de Livros Relacionados
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d