Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 10
Encontre uma equação da tangente à curva no ponto correspondente ao valor do ponto dado. A seguir, trace a curva e a reta tangente
Passo 1
Precisamos encontrar a equação da reta tangente a curva parametrizada:
No ponto:
A equação de uma reta tangente é dada por:
Em que é o coeficiente angular da reta e é dado por:
Chegamos a uma parte que temos uma regra da cadeia, já que temos curvas parametrizadas, que nada mais são que funções compostas. Para calcular a derivada vamos precisar de uma sagacidade agora. (o que eu vou te mostrar um matemático teria um ataque cardíaco, mas funciona para compreender, rsrs )
Ou podemos escrever como
Vou ajustar um pouquinho pra deixar uma coisa evidente
Se queremos a primeira derivada de , então usamos essa formulinha. Agora, para a derivada segunda podemos fazer o seguinte:
Use a forma que achar melhor e que for mais fácil para resolver a nossa equação. Quando terminarmos de calcular a derivada, vamos montar a equação da reta tangente.
Passo 2
Beleza, então temos essas equações
Então vamos arregaçar as mangas e cair dentro
Passo 3
Então nossa derivada fica:
Vamos só lembrar que
A derivada do seno é tabelada, mas precisamos utilizar da regra da cadeia:
Show! Então como fica nossa derivada?
Passo 4
Vamos precisar achar o valor de para achar a inclinação da reta tangente
Se , então nossa equação fica
Então
Chegamos a um ponto que para solucionar nossa equação temos um conjunto de infinitas soluções. Como só precisamos de um ponto, qualquer valor que satisfizer a equação de y já nos é valido. Para descobrir t vamos precisar usar nossa equação para y
Precisamos que .
pode ser qualquer valor que satisfaz y. Vamos escolher então
Beleza! Vamos em frente, vamos plotar esse valor de t na nossa derivada
Lembra como montamos uma equação de reta?
Onde esse são nossos pontos iniciais. E desta vez o nosso enunciado já nos deu os pontos :
Logo nossa equação da reta fica
Passo 5
Por fim, vamos desenhar esse gráfico e ver como ele se comporta geometricamente
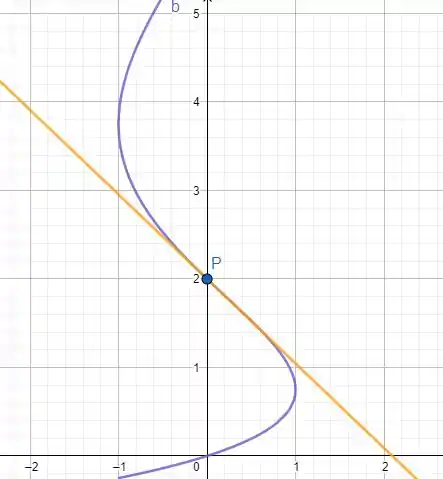
A Curva é nossa função parametrizada. E a reta laranja é nossa reta tangente ao ponto P. Show! Conforme você for resolvendo mais funções, mais vai pegando o jeito. Terminamos por aqui, te vejo na próxima resolução : )