Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.9 - Ex. 6
Nos exercícios de 1 a 8, ache a inclinação da reta tangente à curva dada no ponto, cujo valor de é o indicado. Faça também um esboço do gráfico e da reta tangente.
6.
Passo 1
O enunciado nos pede a inclinação da reta tangente, precisaremos então usar a seguinte equação:
Onde é a inclinação da reta.
Passo 2
Bom primeiro vamos obter o valor dos termos , que se trata da derivada da função r com relação a :
E então substituir na equação da inclinação:
Passo 3
Agora basta substituir o valor de dado no enunciado, na função r:
E substituir e r na equação da inclinação:
A inclinação será:
Passo 4
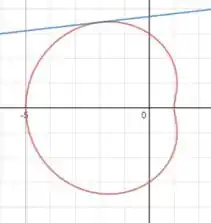
O gráfico da reta tangente então será:
Resposta
Exercícios de Livros Relacionados
Use o exercício 83 para mostrar que o ângulo entre a reta tangente e a reta tadial é ψ = π 4 em cada ponto na curva r = e θ .Ilustre a parte ( a ) traçando, com uma ferramenta gráfica, a curva e a ret
Use a fórmula no Exercício 69(b) para encontrar a curvatura da parábola y = x 2 no ponto ( 1,1 ) .Em que ponto essa parábola tem curvatura máxima?
Se f ' for contínua e f ' t ≠ 0 para a ≤ t ≤ b , mostre que a curva parametrizada x = f t , y = g t , a ≤ t ≤ b , pode ser colocada na forma y = F x .[ S u g e s t ã o : ã Mostre que f - 1 existe.]
Use a fórmula no Exercício 69(a) para calcular a curvatura da cicloide x = θ - s e nθ , y = 1 - cos θ no topo de um dos arcos.
Mostre que a curvatura em cada ponto de uma reta é k = 0 .Mostre que a curvatura em cada ponto do círculo de raio r é k = 1 / r .