Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.9 - Ex. 19

Nos exercícios 9 a 20, determine os pontos nos quais a curva dada tem retas tangentes verticais e horizontais. Faça um esboço do gráfico e mostre essas retas tangentes

19. r 2 = 4 s e n 2 θ

Passo 1

Como o enunciado nos fala sobre retas tangentes, precisaremos aplicar a seguinte equação, para obtermos as inclinações delas:

t g α = t g θ d r d θ + r d r d θ - r t g θ

Reescrevendo a tangente como s e n θ c o s θ , e reorganizando os termos:

t g α = s e n θ d r d θ + r c o s θ c o s θ d r d θ - r s e n θ

Precisamos então calcular d r d θ ,   como tem uma potência quadrada no r, a equação da derivada ficará:

r 2 = 4 s e n 2 θ = 8 s e n θ c o s θ

r d r d θ = 8 c o s 2 θ - s e n 2 θ

Multiplicando e dividindo a equação da inclinação por r:

t g α = s e n θ r d r d θ + r 2 c o s θ c o s θ r d r d θ - r 2 s e n θ

Substituindo os nossos resultados:

t g α = s e n θ ( 4 c o s 2 θ - 4 s e n 2 θ + 8 c o s 2 θ ) c o s θ ( 4 c o s 2 θ - 4 s e n 2 θ + 8 s i n 2 θ )

Utilizando a relação trigonométrica

s e n 2 θ + c o s 2 θ = 1

A nossa equação fica:

t g α = s e n θ ( 4 c o s 2 θ - 1 ) c o s θ 1 - 4 s e n 2 θ

Passo 2

As retas horizontais podem ser obtidas igualando-se o numerador da equação acima a zero, pois assim a inclinação será zero e a reta será horizontal:

s e n θ ( 4 c o s 2 θ - 1 ) = 0

Então teremos três resultados:

s e n θ = 0 → θ = 0   e   θ = π

E

4 c o s 2 θ - 1 = 0

c o s θ = ± 1 2

Para   c o s θ = - 1 2 , θ = 2 π 3

Para c o s θ = 1 2 ,   θ = π 3

Escrevendo r primeiro para θ = 0 :

r = 0

E as coordenadas cartesianas serão:

x = r c o s θ = 0

y = r s e n θ = 0

Para θ =   π o resultado será o mesmo.

Para θ = 2 π 3 , r terá raízes complexas, então iremos descartar esse valor.

Para θ = π 3 :

r = ± 4 s e n 2 π 3 = 12 4

E as coordenadas cartesianas para r positivo:

x = 12 4 c o s π 3 ≅ 0,93

y = 12 4 s e n π 3 ≅ 1,61

E para r negativo:

x = 12 4 c o s π 3 ≅ - 0,93

y = 12 4 s e n π 3 ≅ - 1,61

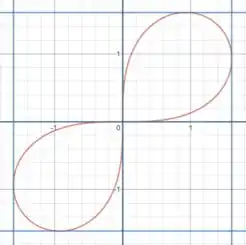
As retas horizontais serão tangentes nos pontos (0,93, 1,61), (-0,93, 1,61) e (0, 0).

Passo 3

Para as retas verticais, precisamos igualar o denominador a zero, para que a inclinação tenda para infinito:

c o s θ 1 - 4 s e n 2 θ = 0

Então teremos:

c o s θ = 0 → θ = π 2

E

1 - 4 s e n 2 θ = 0

s e n θ = ± 1 2 → θ = π 6

Alguns valores possíveis foram descartados, pois não satisfazem a equação de r.

A equação de r para θ = π 2 será:

r 2 = 4 s e n π = 0

Então as coordenadas cartesianas serão:

x = 0

y = 0

Para   θ = π 6 :

r 2 = 4 s e n 2 π 6

r ≅ ± 1,86

Para r positivo, as coordenadas cartesianas serão:

x = 1,86 c o s π 6 ≅ 1,61

y = 1,86 s i n π 6 ≅ 0,93

E para r negativo:

x = - 1,86 c o s π 6 ≅ - 1,61

y = - 1,86 s i n π 6 ≅ - 0,93

E as retas verticais serão tangentes nos pontos (-1,61, -0,93), (1,61, 0,93) e (0 ,0).

Passo 4

O esboço do gráfico então será:

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em quais pontos na curva x = 2 t 3 y = 1 + 4 t - t 2 A reta tangente tem inclinação 1 .
Calcule a área limitada pela curva x = t 2 - 2 t y = t E pelo eixo y .
Com uma ferramenta gráfica, trace a curva x = cos ⁡ t + 2 cos ⁡ 2 t y = sen ⁡ t + 2 s en ⁡ 2 t Para descobrir onde ela intersepta a si mesma. A seguir, encontre a equação para ambas as tangentes nesse
Encontre a inclinação da reta tangente à trocoide x = r θ - d sen ⁡ θ y = r - d cos ⁡ θ Em termos de θ .E mostre que se dr , então a trocoide não tem uma tangente vertical.
Seja P um ponto qualquer (exceto a origem) na curva r = f ( θ ) . Se ψ for o ângulo entre a reta tangente em P e a reta radial em O P mostre que tan ⁡ ψ = r d r d θ Sugestão: observe que ψ = ϕ - θ na