Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.Exercícios práticos - Ex. 32

Encontre equações cartesianas para os círculos nos Exercícios 29-32. Esboce cada círculo no plano coordenado e rotule-o com as equações cartesianas e polares.

Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de equações paramétricas e coordenadas polares.

Vamos agora resolver os exercícios práticos sobre equações polares para equações cartesianas.

Para a equação dada, iremos inicialmente multiplicar por r:

Lembrando que da equação da circunferência temos:

Reescrevemos a equação:

Lembrando ainda que:

Reescrevemos novamente a equação:

Passo 2

Usando o método de completar os quadrados teremos que somar em ambos os lados da equação:

Daí, podemos reescrever como:

Obtendo assim, um círculo de centro e raio dados por:

O esboço do gráfico com suas equações fica:

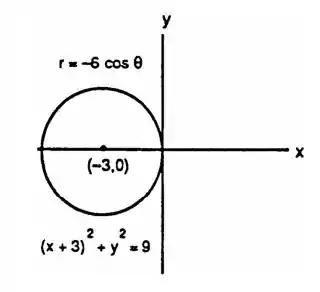
E é isso pessoal. Espero que a resolução tenha sido proveitosa para todos. Até mais.

Resposta

Ver passo a passo.

Exercícios de Livros Relacionados

Encontre equações polares para os círculos nos Exercícios 33-36. Esboce cada círculo no plano coordenado e rotule-o com suas equações cartesianas e polares. x 2 + y 2 + 5 y = 0

Encontre equações cartesianas para os círculos nos Exercícios 29-32. Esboce cada círculo no plano coordenado e rotule-o com as equações cartesianas e polares. r = - 4 sen ⁡ θ

Determine as áreas das superfícies geradas girando as curvas nos Exercícios 21 e 22 em torno dos eixos indicados. x = t 2 2ey = 2 t ; 0 ≤ t ≤ 5 ; e i x ox

Determine as áreas das superfícies geradas girando as curvas nos Exercícios 21 e 22 em torno dos eixos indicados. x = t 2 + 1 2 tey = 4 t ; 1 2 ≤ t ≤ 1 ; e i x oy

Encontre equações polares para os círculos nos Exercícios 33-36. Esboce cada círculo no plano coordenado e rotule-o com suas equações cartesianas e polares. x 2 + y 2 + 4 x = 0