Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.6 - Ex. 10
10.
(a) Encontre a excentricidade, (b) identifique a cônica (c) dê a equação da diretriz, e (d) esboce a cônica.
Passo 1
Tudo bem, pessoal?
Essa questão nos dá a equação de uma cônica e nos pede alguns parâmetros que a caracterizam. Para responder as perguntas, vamos usar a equação geral das cônicas e fazer comparações.
A equação geral de uma cônica é:
Onde é a excentricidade e é a sua diretriz.
Agora vamos usar essa equação para responder as perguntas.
Passo 2
(a) Para encontrarmos a excentricidade, precisamos olhar para o termo que multiplica o seno no denominador.
Como na equação dada temos o 2 somando no denominador, em vez de 1, precisamos ajeitar a equação colocando o 2 em evidência:
E então colocamos para cima para facilitar a visualização:
Pronto, a excentricidade então será:
Passo 3
(b) Podemos identificar a cônica pela excentricidade, como , ela será uma elipse.
Passo 4
(c) Primeiro precisamos encontrar o valor de , para isso, basta compararmos a equação da nossa elipse no passo 1 com a equação geral, o numerador então terá o seguinte valor:
Mas sabemos que , então só pode ser:
E como no denominador da equação temos o termo a diretriz será uma reta horizontal, ou seja, o valor de y será constante:
Passo 5
(d) E o gráfico da cônica será:
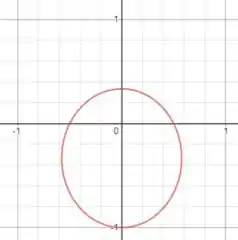
Veja que o semieixo maior da elipse é o eixo , visto que essa elipse tem diretriz .
Podemos ainda determinar as interseções dessa elipse com o eixo . Para isso, vamos fazer e :
Assim, sabemos que a elipse intercepta o eixo nos pontos e .