Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.6 - Ex. 11
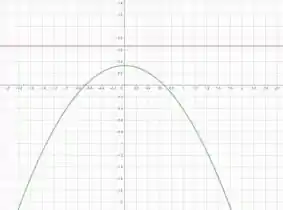
(a) Encontre a excentricidade, (b) identifique a cônica (c) dê a equação da diretriz, e (d) esboce a cônica.
11.
Passo 1
Faaaaala galerinhaaaaa, tudo na paz com vocês? Borá lá!? De início, vamos entender o enunciado e o que a questão está nos solicitando.
Bom, a questão pede que a partir da equação a seguir:
Apresentemos: (a) qual o valor da excentricidade , (b) identificar qual a cônica (se é elipse, parábola ou hipérbole), (c) qual a equação da diretriz (se é uma reta horizontal ou vertical) e por fim (d) realizar um esboço da cônica identificada no item (b).
Sabendo disso, bora começar? 😉
Vamos montar uma estratégia de resolução? Pense comigo! O problema nos forneceu uma equação em coordenadas polares, certo. Então, primeiro precisamos recordar a equação geral de uma cônica, e a partir dela comparar e encontrar o valor dos termos.
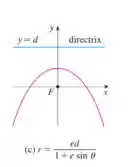
Antes, vamos lembrar dos conceitos e definições de seções cônicas em coordenadas polares. A partir da imagem a seguir (um caso especifico para entender as variáveis na equação polar )
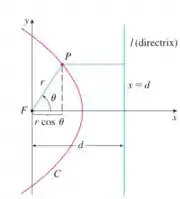
Na imagem, temos uma curva da qual queremos encontrar uma equação em coordenadas polares, e para isso se utiliza de uma reta diretriz que é paralela ao eixo e está a uma distância .
A partir dessas variáveis e as observadas na imagem, foi possível chegar na seguinte expressão geral:
Onde: é a excentricidade, também representado pela razão entre os módulos das distâncias por , ; é a distancia entre o eixo e a reta diretriz.
A partir dessa definição, foi observado outras quatros configurações possíveis, conforme pode ser visto na imagem abaixo
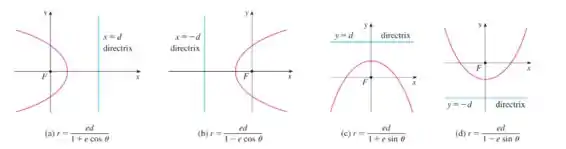
Observe que conforme a posição da curva, ou seja, para onde está voltada a sua concavidade, isso altera a posição da reta diretriz e , e tem como resultado uma equação diferente.
Passo 2
(a). Como podemos encontrar a excentricidade na equação fornecida?
Sabendo dessas informações, vamos analisar a equação fornecida
Primeiro vamos comparar a equação fornecida com as da imagem logo acima, e você concorda que a equação esta equivalente em termos de sinal e do termo trigonométrico com a situação a seguir
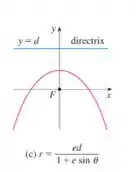
Vamos tentar deixar a equação o mais parecida possível. Então, veja sé possível colocar algum termo em evidência? Sim, podemos colocar o em evidência no denominador, e posterior representar no numerador como uma fração que multiplica , pois é equivalente.
Agora sim, podemos comparar as duas equações e definir qual o valor da excentricidade, basta olharmos o valor que está multiplicando o
Logo, obtemos a excentricidade igual a
Passo 3
(b). Para identificarmos a cônica, qual o passo?
Para determinar a cônica, partimos da análise das seguintes definições para excentricidade
- elipse
- parábola
- hipérbole
Logo, basta olharmos para a excentricidade encontrada anteriormente, como , a cônica será uma parábola.
Passo 4
(c). Qual a equação da diretriz (é uma reta horizontal ou vertical)?
Vamos comparar mais uma vez a equação geral com a equação dada, podemos ver a relação entre os numeradores:
Como sabemos que a excentricidade é , então:
Para sabermos se a diretriz é uma reta horizontal ou vertical, precisamos olhar para o denominador da equação dada, como ele tem o termo a nossa reta será horizontal, e, portanto:
Passo 5
(d). Como podemos fazer um esboço da cônica?
Bom, dos passos anteriores, já sabemos a equação polar e a diretriz
E também sabemos que o gráfico é uma parábola com concavidade para o lado negativo do eixo , conforme a imagem a seguir
Assim, conseguimos plotar o gráfico manualmente se a gente calcular o valor de quando vale , e , pois vamos ter os valores dos raios (distância até a origem).
Os valores de para vão ser os pontos onde a parábola corta o eixo (positivo para e negativo para ):
Já o valor de para é o ponto onde a parábola corta o eixo :
Logo, o gráfico fica:
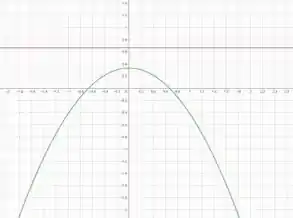
Resposta
(d) 