Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.1 - Ex. 26

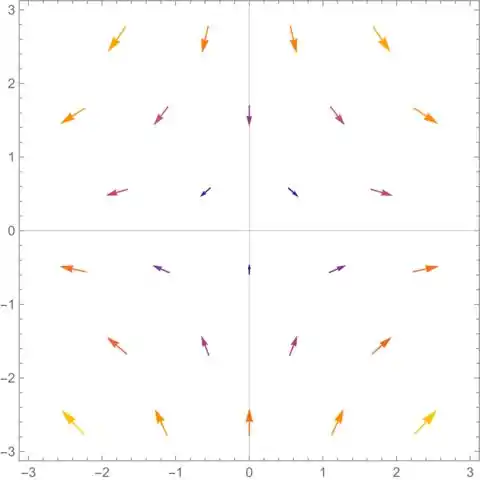
Encontre o campo vetorial gradiente ∇ f de f e o esboce.

f x , y = 1 2 ( x 2 - y 2 )

Passo 1

E aii, pessoal!

Nessa questão, a gente precisa achar o gradiente de f e esboçar.

f x , y = 1 2 ( x 2 - y 2 )

Pra isso, vamos lembrar quem é o gradiente:

∇ f x , y = f x   i → + f y   j →

Vamos começar calculando as derivadas parciais, pra definir o campo gradiente.

Daí, vamos analisar ele pra entender como ele se comporta conforme mudamos o ponto x , y .

Passo 2

Começamos derivando em função de x , com y constante:

f x = ∂ 1 2 x 2 - y 2 ∂ x = 1 2 ∙ ∂ x 2 - y 2 ∂ x

= 1 2 ∙ 2 x

Então

f x = x

Agora derivando em função de y , considerando x constante:

f y = ∂ 1 2 x 2 - y 2 ∂ y = 1 2 ∙ ∂ x 2 - y 2 ∂ y

= 1 2 ∙ - 2 y

Então

f y = - y

E o gradiente fica:

∇ f x , y = x   i → - y   j →

Passo 3

Agora a gente vai analisar esse campo.

Percebe que como a primeira coordenada é exatamente x , ela vai ter o mesmo valor que a coordenada do ponto.

∇ f x , y = x   i → - y   j →

Ou seja, à direita do eixo y , os vetores apontam pra direita ( x > 0 ), e à esquerda apontam pra esquerda ( x < 0 ).

Já com relação à segunda coordenada, ela vale - y , então é o oposto da coordenada do ponto.

∇ f x , y = x   i → - y   j →

Assim, acima do eixo x , y > 0 ⇒ - y < 0 , então o vetor aponta pra baixo. Abaixo, y < 0 ⇒ - y > 0 , e o vetor aponta pra cima.

Com isso, desenhamos o campo:

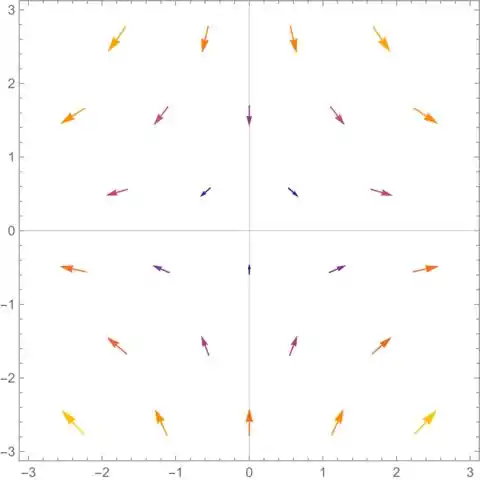
Resposta

∇ f x , y = x   i → - y   j →

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Case as funções com os desenhos de seus campos de vetor gradiente (rotulados de I-IV). Dê razões para suas escolhas. f x , y = x y
Esboce o campo vetorial F, desenhando um diagrama como o da Figura 5 ou da Figura 9 F x , y , z = j
Esboce o campo vetorial F, desenhando um diagrama como o da Figura 5 ou da Figura 9 F x , y , z = z j
Esboce o campo vetorial F, desenhando um diagrama como o da Figura 5 ou da Figura 9 F x , y , z = y j
Esboce o campo vetorial F, desenhando um diagrama como o da Figura 5 ou da Figura 9 F x , y , z = j - i