Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.6 - Ex. 13
(a) Encontre a excentricidade, (b) identifique a cônica (c) dê a equação da diretriz, e (d) esboce a cônica.
13.
Passo 1
Faaala, pessoal! Essa questão da pra gente uma equação que representa uma cônica, e pede várias coisas:
- a excentricidade, que é aquele que aparece na equação geral:
- qual cônica é (parábola, elipse ou hipérbole)
- a equação da diretriz, que é aquela reta que define a cônica
- um esboço da cônica, que vai depender de tudo isso que a gente achar nos outros itens:
Pra encontrar esse valor, a gente vai comparar a equação que ele deu com a equação geral
Lembra que o é sempre um valor positivo!!
Isso vai depender do valor de que a gente encontrar:
: elipse
: parábola
: hipérbole
Ela pode ter esses formatos:
O é o mesmo da equação geral, e a gente vai descobrir ele igual o . Pra saber qual o formato da equação, a gente vai precisar olhar pro denominador da equação da cônica ( ou ): o ou e o sinal vão dizer pra gente o formato:
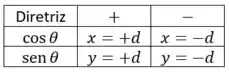
- O valor de vai indicar qual cônica é
- A equação da diretriz vai indicar a direção dessa cônica
- Sabendo a direção da cônica, a gente consegue calcular os vértices:
Se a diretriz for , os raios dos vértices são os valores de para e , enquanto e vai nos indicar os pontos onde a cônica corta o eixo .
Se a diretriz for , os raios dos vértices são os valores de para e , enquanto e vai nos indicar os pontos onde a cônica corta o eixo .
Então vamos fazer por partes!
Passo 2
(a) Vamos então comparar a equação da cônica com a equação geral:
Comparando com a equação que ele deu:
Ela tem uma cara parecida com a primeira equação, certo? O único problema é esse no lugar do . Pra resolver isso, a gente pode colocar esse em evidência:
Agora, vamos colocar o de fora para cima e depois simplificamos tudo:
Comparando com a equação geral:
Podemos encontrar a excentricidade:
Passo 3
(b) Como a excentricidade é menor que a cônica é uma elipse.
Passo 4
(c) Para acharmos a diretriz, primeiro comparamos o numerador da equação geral do Passo com a equação do enunciado:
Então:
Mas sabemos que , assim:
será:
Como o termo o denominador é , podemos dizer que a diretriz é vertical e está à direita da elipse (), pelo valor de , a equação será:
Passo 5
(d) Bom, a gente já sabe que o gráfico vai ser uma elipse, né? Mas como vamos esboçar essa cônica?
Como a diretriz é do tipo , a gente sabe que essa elipse está deslocada ao longo do eixo (isto é, os focos têm ).
Tá, mas o que eu faço com essa informação?
Se a gente calcular o valor de quando vale e , vamos ter os valores dos raios (distância até a origem) dos vértices da elipse:
Além disso, os valores de para e vão ser os pontos onde a elipse corta o eixo (positivo para e negativo para ):
Com essas informações, já da pra gente esboçar o gráfico da cônica:
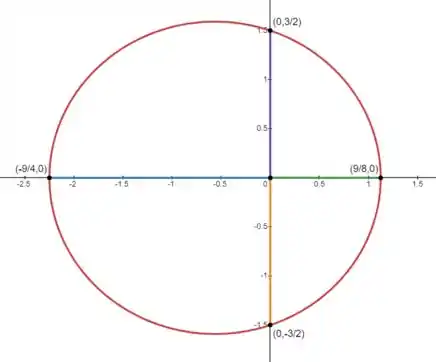
As retas verde e azul são os raios para e .
As retas roxa e laranja são os raios para e .
A elipse vermelha é a cônica.
Resposta
