Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.6 - Ex. 16
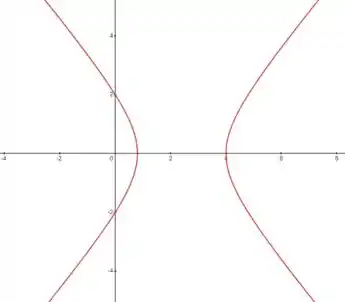
(a) Encontre a excentricidade, (b) identifique a cônica (c) dê a equação da diretriz, e (d) esboce a cônica.
16.
Passo 1
E aii, vamos pra mais uma?
A questão da pra gente uma equação que representa uma cônica, e pede várias coisas:
- a excentricidade – aquele que aparece na equação geral, que pode ter um desses formatos:
- qual cônica é (parábola, elipse ou hipérbole)
- a equação da diretriz (que é aquela reta que define a cônica)
- um esboço da cônica, que depende dos itens (b) e (c):
Se a gente comparar a equação do enunciado com essas ai, a gente acha o
Lembra que o é sempre um valor positivo!!
Isso depende do valor de que a gente achar em (a):
: elipse
: parábola
: hipérbole
Ela pode ter esses formatos:
O é o da equação geral, que a gente vai achar igual o .
O ou vai depender se aparece ou na equação da cônica, e o sinal depende do sinal que aparece nesse termo ( ou ):
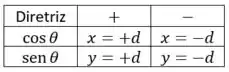
- O valor de vai indicar qual cônica é
- A equação da diretriz vai indicar a direção dessa cônica
- Sabendo a direção da cônica, a gente consegue calcular os vértices:
Se a diretriz for , os raios dos vértices são os valores de para e , enquanto e vai nos indicar os pontos onde a cônica corta o eixo .
Se a diretriz for , os raios dos vértices são os valores de para e , enquanto e vai nos indicar os pontos onde a cônica corta o eixo .
Então vamos resolver!
Passo 2
(a) Bom, vamos primeiro olhar para a equação geral das cônica. Como temos no denominador uma expressão do tipo , vamos comparar com essa equação geral:
Mas devemos tomar cuidado com a maneira como a equação dada está escrita, ela não está na mesma forma que a equação geral, vamos então reescrevê-la, colocando o em evidência no denominador:
E simplificamos:
Comparando com a equação geral:
Podemos tirar a excentricidade, que será:
Passo 3
(b) Como essa excentricidade é maior que 1, a cônica será uma hipérbole.
Passo 4
(c) A primeira coisa pra achar a diretriz é calcular o valor de , e pra isso a gente compara a equação geral com a equação do enunciado, como no Passo :
Comparando os numeradores, temos:
Já que sabemos o valor de , ficamos com:
Como a equação da nossa hipérbole possui denominador , a diretriz será constante em , e estará à direita do foco (será positiva), então usando o valor de :
Passo 5
(d) Como vimos no Passo , esse gráfico vai ser uma hipérbole. Agora, como vai ser essa hipérbole?!
Bom, essa hipérbole tem uma diretriz do tipo , ou seja, ela está deslocada ao longo do eixo .
Isso diz pra gente que pra achar os raios dos vértices é só calcular os valores de para e :
Já os valores de quando vale e vão nos dar os pontos onde a cônica corta o eixo (positivo para e negativo para ):
Com isso, o gráfico da cônica será:
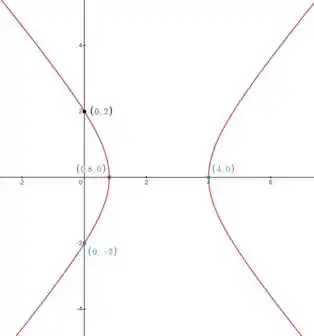
Os valores que a gente achou são esses pontos que estão destacados. Pra fazer a parte da esquerda da hipérbole, eles são suficientes.
A parte da direita a gente consegue fazer em seguida, porque é só espelhar! 😊
Resposta
