14.
(a) Encontre a excentricidade, (b) identifique a cônica (c) dê a equação da diretriz, e (d) esboce a cônica.
Passo 1
Tudo bem, pessoal?
Essa questão nos dá a equação de uma cônica e nos pede alguns parâmetros que a caracterizam. Para responder as perguntas, vamos usar a equação geral das cônicas e fazer comparações.
A equação geral de uma cônica é:
Onde é a excentricidade e é a sua diretriz.
Agora vamos usar essa equação para responder as perguntas.
Passo 2
(a) Podemos encontrar a excentricidade comparando a equação do enunciado com uma das equações gerais das cônicas:
O que multiplica a função seno é a excentricidade, mas a equação dada não está na mesma forma da equação geral, vamos ajeitá-la para que fique o mais parecido possível. Colocamos o 3 em evidência no denominador:
E colocamos ele para cima, porque isso vai ajudar a gente a encontrar a diretriz na letra (c):
Pronto, agora basta olharmos para o quê multiplica a função seno, isso será a excentricidade, assim:
Passo 3
(b) Como a excentricidade é 1, essa cônica é uma parábola.
Essa será a equação da diretriz.
Passo 4
(c) Para acharmos a equação da diretriz, precisamos primeiro encontrar , para isso, comparamos o numerador da equação geral com o da equação dada, teremos:
E já que sabemos o valor da excentricidade:
Agora precisamos saber se a diretriz é horizontal ou vertical, como no denominador temos o termo , significa que y é constante, ou seja, a reta é vertical, e como o sinal é negativo, o valor de y também será, então:
Passo 5
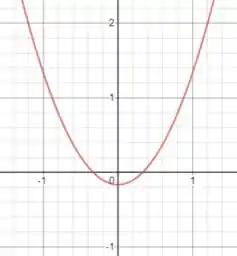
Os pontos onde essa parábola cruza o eixo são dados por e .
Vamos calcular...
Então os pontos são: e .
O vértice da parábola é calculado para
Ou seja, o vértice é .
Juntando todas essas informações nós podemos fazer o gráfico da parábola: