Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.2 - Ex. 8
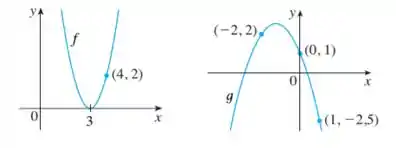
Encontre expressões para as funções quadráticas cujos gráficos são mostrados abaixo.
Passo 1
E aí, tudo tranquilo?
Pronto pra resolver mais uma questão?
Não precisa ficar desesperado, estarei te ajudando a resolver essa atividade.
Aqui a gente vai, a partir da análise do gráfico para encontrar qual é a função mostrada. A gente tem ali funções do segundo grau.
Essas funções são da forma:
As constantes desempenham um papel importante no gráfico.
A constante é o ponto onde o gráfico toca o eixo . Então:
A constante nos diz a direção da parábola, se tivermos a nossa parábola terá a direção do eixo positivo de , mas caso tivermos nossa parábola terá a direção do eixo negativo de .
Outro ponto interessante para a gente é o vértice de uma função do segundo grau, ele pode ser encontrado:
E
E é o ponto onde a função atinge o valor máximo ou mínimo, dependendo da concavidade da parábola descrita pela função.
Com ajuda dessas informações, e com alguns pontos indicados no gráfico, poderemos criar um sistema de equações e assim conseguirmos encontrar cada uma das constantes.
Veja só! 👀
Passo 2
A gente vai começar trabalhando com esse cara aqui:
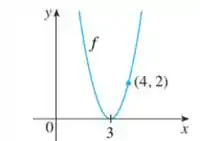
O que a gente pode verificar de cara é que temos a parábola tocando em só um ponto no eixo .
Isso quer dizer que as duas raízes da nossa função de segundo grau são iguais e iguais à .
Como a função de segundo grau é um polinômio, todo polinômio pode ser escrito da seguinte forma:
Sendo que aqui é o termo que controla a quão ‘aberta’ e ‘fechada’ será nossa parábola, pois existem uma família infinita de funções do segundo grau com raízes iguais a , apenas mudando o valor de , o que queremos saber é qual dessas infinitas é a nossa.
Onde os representam as raízes desse polinômio, fechou? A gente pode, então, escrever a nossa função do segundo grau assim:
Tranquilo até aqui? 😉
Passo 3
Agora, temos que encontrar o valor de para termos a nossa função do segundo grau escrita completamente.
A gente pode fazer isso usando a equação que a gente tem e mais o ponto que é dado! Sabemos que esse ponto pertence a parábola, sendo assim iremos substituir.
saca só:
A gente pode, então, escrever a nossa equação:
E expandir ela para ficar na forma do segundo grau:
Bacana, não é? 😬
Passo 4
Agora, nós vamos lidar com esse cara aqui:
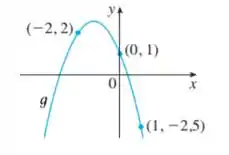
Podemos sempre definir um polinômio com grau a partir de pontos, ou seja: como temos uma função do segundo grau (), podemos achar sua expressão através dos pontos que nos deram.
Beleza até aqui?
Temos os pontos , e .
Agora, vamos jogar cada ponto na expressão genérica de uma função do segundo grau .
Para :
Para :
Para :
Bora continuar! 😁
Passo 5
Agora, vamos organizar as três equações que encontramos:
Temos que resolver esse sistema de três equações, e aí vamos ter os valores de e . Uma das equações já é o próprio valor de ! A gente pode substituir nas nossas outras duas equações já, saca só:
Temos então que:
E iremos substituir:
Substituindo isso em:
Estamos quase lá! 👀
Pronto! Agora temos os valores de e . Substituindo na fórmula da função do segundo grau, vamos ter que:
E fim! O que achou? Responde AÍ! 😊
Resposta
As funções que expressam os gráficos são (para o gráfico da esquerda) e (para o gráfico da direita).