Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.6 - Ex. 35b
Encontre o valor exato de cada expressão.
Passo 1
E aí, tudo bem? Aqui precisamos calcular:
Pra resolver esse problema vamos usar a definição de logaritmo:
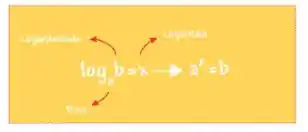
E também é bom ter em mente as propriedades:
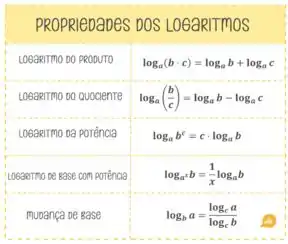
A ideia aqui é ir manipulando a função até encontramos alguma coisa que a gente consiga calcular!
Passo 2
Mãos à massa então, temos:
A primeira manipulação não é uma propriedade dos logs, quando a gente tem alguém no denominador podemos subir ele adicionando o expoente . Temos que:
Além disso temos que:
Então:
Passo 3
Aqui a gente pode usar a propriedade de potência:
Passo 4
Beleza, agora vamos pensar na definição de log. Aqui temos:
Então:
Com isso:
Chegamos então em:
Aweeee!
Resposta
Exercícios de Livros Relacionados
Encontre o valor exato de cada expressão.e^(- 2 . ln 5) ln ( ln e^(e^(10)) )
Encontre o valor exato de cada expressão.log_2 6 - log_2 15 + log_2 20 log_3 100 - log_3 18 - log_3 50
Determine o domínio.f (x) = log_x 3
Determine o domínio.f (x) = log_2 (x + 1)
Determine o domínio.f (x) = log_3 |x|