Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 59
Encontre uma fórmula para a função descrita e obtenha seu domínio.
Expresse a área de um triângulo equilátero como uma função do comprimento de um lado.
Passo 1
E aí, tudo bom?!
Aqui a gente tem que escrever uma fórmula pra calcular a área de um triângulo equilátero a partir do comprimento de um lado .
Só pra a gente lembrar, o triângulo equilátero é assim:
Ele tem três lados e três ângulos iguais! Pra a gente chegar na área vamos sair da fórmula geral da área de um triângulo:
Onde é a base e é a altura. Vamos manipular essa função e usar as informações que sabemos sobre o triângulo equilátero pra deixar tudo em função de !
Depois disso temos que dizer qual é o domínio da nossa função, que aqui vai ser todos os valores de que são “permitidos”, ou seja, que podem ser substituídos na função!
Bora colocar a mão na massa?!
Passo 2
Beleza, agora vamos pensar.... Podemos dividir esse triângulo no meio e vamos ter dois triângulos retângulos. Certo?!
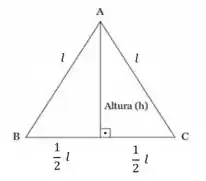
Ok...então podemos usar o teorema de Pitágoras pra escrever a altura em função dos lados:
Isolando a altura:
Isso nos dá:
Podemos tirar o e o da raiz:
Passo 3
Agora vamos voltar pra fórmula geral da área do triângulo:
Sabemos quem é a altura, já a base a gente pode chamar de , uma vez que todos os lados são iguais. Inclusive a base. Então:
Vamos dar aquela arrumadinha:
Então a nossa função é:
Prontinho!
Passo 4
Pra acabar, precisamos determinar o domínio de :
Olhando a função vemos que não existe nenhuma restrição pra , ele não ta dentro de uma raiz, nem no denominador, por exemplo. Então podemos dizer que esta função tem o domínio dos reais!