Um pedaço de fio com de comprimento é cortado em duas partes. Uma parte é dobrada no formato de um quadrado, ao passo que a outra é dobrada na forma de um triângulo equilátero. Como deve ser cortado o fio de forma que a área total englobada seja:
(a) máxima?
(b) mínima?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado nos disse que um pedaço de fio com de comprimento foi cortado em duas partes. Uma parte foi dobrada no formato de um quadrado e a outra foi dobrada na forma de um triângulo equilátero. Ele quer saber como deve ser cortado o fio de forma que a área total englobada seja (a) máxima ou (b) mínima.
A primeira coisa é esboçar as informações dadas num desenho:
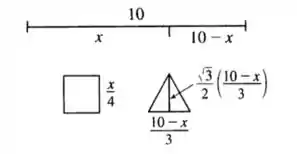
Cada lado do quadrado vale
porque o tamanho de fio é dividido pelos quatro lados, e o triângulo usa a mesma lógica. A altura do triângulo possui esse valor por conta da propriedade geométrica que nos diz que
O exercício quer a área total máxima e mínima dessas figuras, então vamos buscar escrever uma expressão para essa área e encontrar os pontos críticos da função, verificando se eles são de máximo ou mínimo.
Vamos lá!
Passo 2
Somando a área do quadrado com a área do triângulo, vamos ter a área total:
Lembrando que a área do quadrado é dada por:
E a área do triângulo será:
Assim, a área total será:
Calculando esse produto nos colchetes e simplificando, vamos ter:
onde, porque o fio tem de comprimento.
E essa é a expressão da área das figuras.
Passo 3
Como está dependendo de apenas uma variável, já é possível derivar e igualar a zero para encontrar seus pontos críticos. Como
Derivando a equação em relação a , vamos ter:
E igualando esse resultado a zero:
Aplicando a distributiva no produto:
Tirando o MMC:
Colocando em evidência:
E isolando , temos:
Passo 4
Como pode variar entre zero e dez, substituímos esses dois valores na equação de área, para encontrar seus valores extremos:
Agora substituindo , temos:
Só falta verificar o valor da área no ponto crítico . Assim, temos:
Passo 5
O Teorema de Weierstrass nos diz que uma função contínua necessariamente tem valores mínimo e máximo absolutos em um intervalo fechado. Esses valores extremos são pontos máximos ou mínimos relativos dentro do intervalo, ou pontos nas extremidades do intervalo.
Dessa forma, podemos apenas comparar os valores que obtivemos no passo anterior e verificar quais deles representam pontos de máximo ou de mínimo.
Repare que a área máxima encontrada acontece quando , e vale , ou seja, toda a corda é usada para o quadrado.
Além disso, comparando os resultados, a gente consegue perceber que a área mínima encontrada acontece quando , e vale .
Valeu, galera! Até a próxima! 😉
Resposta
(a) área máxima:
(b) área mínima: