- Encontre a função comprimento de arco para a curva com o ponto inicial .
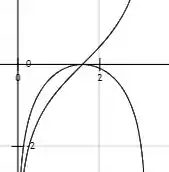
- Trace a curva e faça o gráfico de sua função comprimento de arco na mesma tela.
Passo 1
A nossa função é a . O primeiro passo para escrevermos nossa função de comprimento de arco é encontrar a primeira derivada da função. Assim,
O segundo passo é escrevermos . Portanto,
Note que temos aqui uma identidade trigonométrica! Sabemos que . Assim,
Passo 2
Por fim, vamos escrever a nossa função de comprimento de arco!
Passo 3
Vamos agora plotar aqui a função e a função do comprimento de arco no mesmo gráfico. Aqui, vemos que cresce no intervalo e que e . Assim,
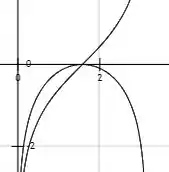
Resposta
- ;