Encontre a inclinação da reta tangente à trocoide x = r θ - d sen ⁡ θ y = r - d cos ⁡ θ Em termos de θ .E mostre que se dr , então a trocoide não tem uma tangente vertical.

d y d x = d sen ⁡ θ r - d cos ⁡ θ

Enunciado

A inclinação da reta tangente à curva é dada por

Assim, precisamos encontrar as derivadas de e em relação a e substituir nessa fórmula.

Vamo começar pela derivada de :

Agora a derivada de :

Substituindo na fórmula

E tá aí a inclinação da nossa reta tangente em termos do parâmetro .

Agora precisamos mostrar que se , ou seja, se nossa trocoide é interna, ela não tem uma reta tangente vertical.

A reta tangente é vertical quando

Assim, devemos provar que para , nunca será igual a zero. Sacou?

Sabemos que

Temos a seguinte situação

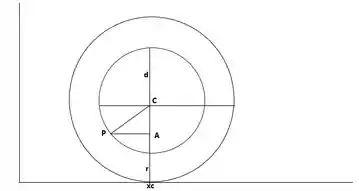
E as coordenadas do nosso ponto são a parametrização da trocoide.

Relembrando rapidamente, temos

E, do triangulo :

Agora voltando a nossa questão, já que temos

Podemos dizer que

Então

Fazendo em todos os membros da inequação:

Isso quer dizer que

Ou seja, nunca valerá zero.

E isso significa que não há tangente vertical.