Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.2 - Ex. 26
Com uma ferramenta gráfica, trace a curva
Para descobrir onde ela intersepta a si mesma. A seguir, encontre a equação para ambas as tangentes nesse ponto.
Passo 1
Beleza, lá vamo nós pro nosso querido Winplot traçar essa curva aí.
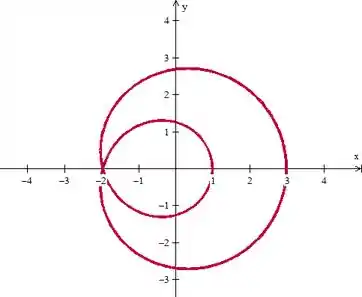
E com isso a gente vê que a curva se intersepta no ponto:
PS: como sempre, se a gente não tivesse com um pc por perto pra ajudar a traçar a curva, poderíamos só ter chutados vários valores para e substituir na curva e com isso obteríamos vários pontos. Daí era só plotar esses pontos e ligar tudo pra ter a curva. É um processo mais trabalhoso e rudimentar, mas funciona também, tá bem?
Passo 2
Show, agora que temos nosso ponto, bora descobrir a reta tangente nesse ponto.
O vetor tangente à curva é dado por
Assim, precisamos encontrar as derivadas de e em relação a e substituir nessa fórmula.
Passo 3
Vamo começar pela derivada de :
Agora a derivada de :
Substituindo na fórmula
Passo 4
Agora a gente precisa descobrir o valor do parâmetro correspondente ao ponto de tangencia . Para isso é igualar o ponto à parametrização da curva e resolver o sistema.
Das formulas o ângulo duplo, substituindo na primeira equação, temos:
Ou
Ou seja, temos dois valores possíveis para correspondentes ao ponto .
Passo 5
Substituindo no vetor tangente, temos:
Para
Para :
Assim, temos dois vetores tangentes, logo, vamos ter duas retas tangentes no ponto .
Passo 6
As equações da reta tangente no ponto ficam:
E
Resposta
As retas tangentes são
E