Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.7 - Ex. 9

  1. Encontre a inclinação da tangente à curva y = 3 + 4 x 2 - 2 x 3 no ponto onde x = a
  2. Encontre as equações das retas tangentes nos pontos 1,5   e   ( 2,3 )  
  3. Faça o gráfico das curvas e de ambas as retas tangentes em uma mesma tela

Passo 1

Olá, querido estudante. Temos aqui uma situação em que deveremos encontrar a equação da reta tangente a curva

y = 3 + 4 x 2 - 2 x 3

Num ponto genérico x = a .

Para isso, iremos utilizar a equação do coeficiente angular da reta tangente m :

m = lim h → 0 ⁡ f a + h - f a h

Onde no nosso caso:

y = f ( x ) = 3 + 4 x 2 - 2 x 3

E o m que encontramos é a inclinação que estamos procurando. Já para encontrarmos a equação da reta, iremos utilizar a fórmula:

y - y 1 = m x - x 1

Onde x 1 , y 1 é o ponto tangente que nos é dado no enunciado.

Vamos a resolução.

Passo 2

A letra (a) pede pra a gente encontrar a inclinação da tangente à curva y = 3 + 4 x 2 - 2 x 3 no ponto onde x = a , então bora lá!

m = lim h → 0 ⁡ f a + h - f a h

Substituindo:

y = f ( x ) = 3 + 4 x 2 - 2 x 3

f a + h = 3 + 4 a + h 2 - 2 a + h 3

Agora substituindo todo mundo no limite:

lim h → 0 ⁡ 3 + 4 a + h 2 - 2 a + h 3 - 3 - 4 a 2 + 2 a 3 h

Realizando os produtos notáveis:

= lim h → 0 ⁡ 3 + 4 a 2 + 8 a h + 4 h 2 - 2 a 3 - 6 a 2 h - 6 a h 2 - 2 h 3 - 3 - 4 a 2 + 2 a 3 h

Simplificando os termos semelhantes:

= lim h → 0 ⁡ 8 a h + 4 h 2 - 6 a 2 h - 6 a h 2 - 2 h 3 h

colocando h em evidência:

= lim h → 0 ⁡ h 8 a + 4 h - 6 a 2 - 6 a h - 2 h 2 h

Simplificando

= lim h → 0 ⁡ 8 a + 4 h - 6 a 2 - 6 a h - 2 h 2 = 8 a - 6 a 2

Calculando agora nosso limite:

m = a ( 8 - 6 a )

Temos então nosso coeficiente angular.

Passo 3

Letra b)

Agora encontraremos a equação da reta tangente no ponto ( 1,5 ) , basta substituir x = a = 1 na inclinação da tangente encontrada no item (a):

m = 1 ⋅ ( 8 - 6 ⋅ 1 )

m = 2

Daí, a equação da reta tangente será:

y - y 1 = m ( x - x 1 )

Substituindo os valores:

y - 5 = 2 ( x - 1 )

y = 2 x - 2 + 5

y = 2 x + 3

Agora encontraremos a equação da reta tangente no ponto ( 2,3 ) , basta substituir x = a = 2 na inclinação da tangente encontrada no item (a):

m = 2 ⋅ ( 8 - 6 ⋅ 2 )

m = - 8

Daí, a equação da reta tangente será

y - y 1 = m ( x - x 1 )

Substituindo os valores:

y - 3 = - 8 ⋅ ( x - 2 )

y = - 8 x + 16 + 3

y = - 8 x + 19

Passo 4

Letra c)

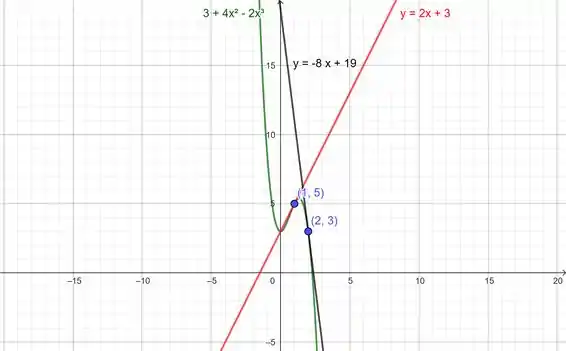
Por fim precisamos fazer o esboço da curva y = 3 + 4 x 2 - 2 x 3 e das retas tangentes y = 2 x + 3 e y = - 8 x + 19 . Para isso vamos fazer uma tabelinha:

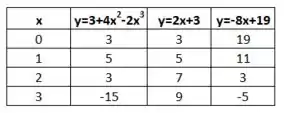
Lembrando que os pontos das retas tangentes são ( 1,5 ) e ( 2,3 ) , então é importante escolhermos um intervalo que contenha esses pontos. Agora finalmente plotamos o gráfico:

Resposta

m = a ( 8 - 6 a )

y = 2 x + 3

y = - 8 x + 19

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 13 a 20, ache uma equação da reta tangente a curva dada, no ponto indicado. Faça um esboço da curva com a reta tangente e a reta norma.16)y = x 2 + 2 x + 1 ; ( 1,4 )
Nos exercícios de 13 a 20, ache uma equação da reta tangente a curva dada, no ponto indicado. Faça um esboço da curva com a reta tangente e a reta norma.14)y = x 2 - x + 2 ; ( 2,4 )
Nos exercícios de 13 a 20, ache uma equação da reta tangente a curva dada, no ponto indicado. Faça um esboço da curva com a reta tangente e a reta norma.13)y = x 2 - 4 x - 5 ; ( - 2,7 )
Nos exercícios de 13 a 20, ache uma equação da reta tangente a curva dada, no ponto indicado. Faça um esboço da curva com a reta tangente e a reta norma.19)y = x 4 - 4 x ; ( 0,0 )
Nos exercícios de 13 a 20, ache uma equação da reta tangente a curva dada, no ponto indicado. Faça um esboço da curva com a reta tangente e a reta norma.15)y = 1 8 x 3 ; ( 4,8 )