Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.3 - Ex. 66
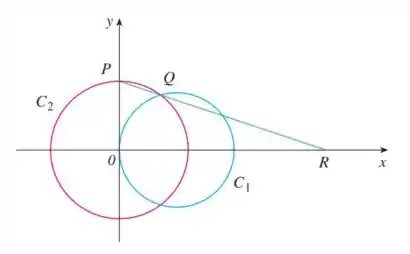
A figura mostra um círculo fixo de equação e um círculo , a ser escolhido, com raio e centro na origem. é o ponto , é o ponto de intersecção superior dos dois círculos, e é o ponto de intersecção da reta com o eixo . O que acontecerá com quando se contrair, isto é, quando ⁺?
Passo 1
Eaee, belezinha??? Bom... a questão nos dá a seguinte figura:
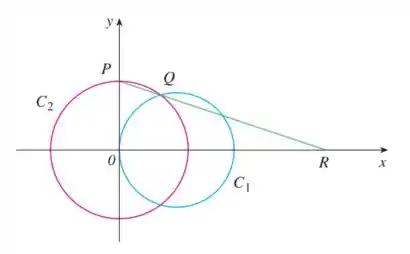
Onde o círculo tem a seguinte equação:
O círculo não tem equação, mas temos os seguintes dados:
- raio ;
- centro na origem;
- é o ponto ;
- é o ponto de intersecção superior dos dois círculos;
- é o ponto de intersecção da reta com o eixo .
Queremos saber o que acontecerá com quando se contrair, isto é, quando ⁺.
Para isso, iremos utilizar do limite para analisar essa situação prática. Lembrando que quando falamos ⁺, esse sinal de + indica que estamos nos aproximando de 0 pela direita, ou seja, por valores maiores que 0. Isso é um limite lateral!
Primeiro vamos achar as coordenadas de e em função de , assim vai ser possível achar a equação da reta determinada por esses dois pontos, e assim nós achamos o ponto que intercepta, o ponto , e fazemos o limite de , vamos lá!!
Passo 2
Temos as coordenadas de como , e o ponto é o ponto de intersecção dos dois círculos, e . Vamos combinar as duas equações
Isolando o da primeira:
Substituindo na segunda:
E simplificando:
Temos a primeira coordenada do ponto .
Passo 3
Agora vamos substituir o valor de que acabamos de achar na equação do círculo:
Vamos isolar o termo , assim achamos a segunda coordenada do ponto:
Passo 4
Agora que temos as coordenadas dos dois pontos, vamos achar o coeficiente angular:
E aplicar na equação da reta:
Para achar a coordenada nós colocamos , subsitituimos na equação e isolamos o :
Portanto,
Passo 5
Por último nós tomamos o limite com , vamos lá:
Assim, temos que a posição máxima que pode chegar é o ponto .
Resposta
O ponto chegará ao ponto máximo, que é o ponto .