Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.7 - Ex. 2
Faça o gráfico da curva nas janelas por , por e por . Dando um zoom no ponto , o que você percebe na curva?
Passo 1
Opaaa! Bora resolver esse problema!
O enunciado pede pra a gente desenhar um gráfico da função considerando as seguintes janelas:
Ou seja, vamos plotar:
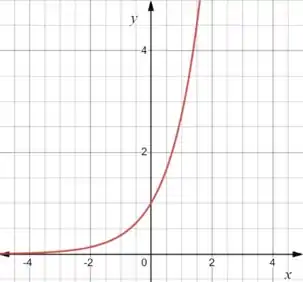
Agora vamos dar um zoom em cada janela e tirar novos prints!
Veja só! 😉
Passo 2
Fazendo o gráfico da primeira janela temos:
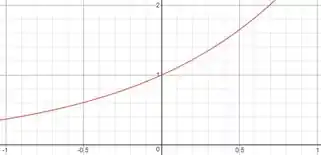
Na segunda janela :
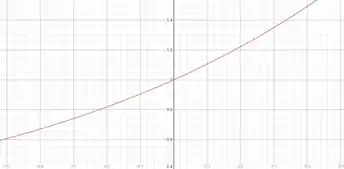
E por fim, na terceira janela, :
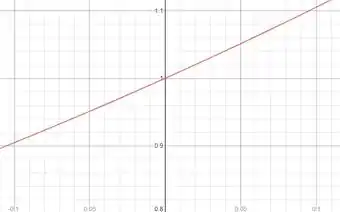
Tranquilo até aqui? 👀
Passo 3
De uma janela para outra é como se a gente tivesse dando um zoom maior na curva! Quando um zoom é dado no ponto, a curva se aproxima cada vez mais de uma reta
Legal, né? O que achou? Responde Aí! 😁
Resposta
Quanto maior o zoom, mais a curva se aproxima de uma reta.
Exercícios de Livros Relacionados
4) Encontre a linearização L ( x ) da função em a . f x = x 3 / 4 , a = 16
3) Encontre a linearização L ( x ) da função em a . f x = cos x , a = π / 2
1) Encontre a linearização L ( x ) da função em a . f x = x 3 , a = 1
2) Encontre a linearização L ( x ) da função em a . f x = ln x , a = 1
Encontre a aproximação linear da função g x =1 + x 3 em a = 0 e use-a para aproximar os números 0,95 3 e 1,1 3 . Ilustre fazendo os gráficos de g e da reta tangente