Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.1 - Ex. 13
Nos exercícios de 13 a 20, ache uma equação da reta tangente a curva dada, no ponto indicado. Faça um esboço da curva com a reta tangente e a reta norma.
13)
Passo 1
Primeiramente iremos calcular a inclinação da reta tangente. Para isso utilizamos a seguinte definição:
Assumindo que , temos:
e
Logo, aplicando na definição:
Desenvolvendo o produto notável e simplificando, temos:
Substituindo o x do ponto:
Passo 2
Agora para encontrarmos a equação da reta tangente no ponto dado, utilizamos a equação fundamental da reta:
Substituindo o coeficiente angular e o ponto dado, temos:
Colocando no formato de equação geral da reta, temos:
Passo 3
Agora faremos o esboço do gráfico com a reta tangente e a reta normal no ponto dado é:
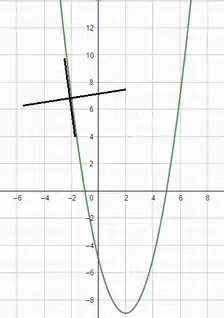
Resposta
Equação da reta tangente:
Gráfico:
Exercícios de Livros Relacionados
Seja y = f x definida e derivável num intervalo contendo 1 e suponha que f seja dada implicitamente pela equação y 3 + x 2 y = 130 . Determine as equações das retas tangente e normal ao gráfico de f ,
Expresse d y d x em termos de x e de y , onde y = y x é uma função derivável, dada implicitamente pela equação dada. y 3 + sen x y = 1 e y + x y = x y x + x = y 2 x cos y + y cos x = 2
O gráfico da função abaixo possui alguma tangente horizontal no intervalo 0 ≤ x ≤ 2 π ? Se sim, onde? Se não, por quê? Visualiza os resultados representando as funções com uma ferramenta gráfica y = 2
O gráfico da função abaixo possui alguma tangente horizontal no intervalo 0 ≤ x ≤ 2 π ? Se sim, onde? Se não, por quê? Visualiza os resultados representando as funções com uma ferramenta gráfica y = x
O gráfico da função abaixo possui alguma tangente horizontal no intervalo 0 ≤ x ≤ 2 π ? Se sim, onde? Se não, por quê? Visualiza os resultados representando as funções com uma ferramenta gráfica y = x