Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 15

  1. Encontre os intervalos nos quais f é crescente ou decrescente.
  2. Encontre os valores máximo e mínimo local de f .
  3. Encontre os intervalos de concavidade e os pontos de inflexão.

f x = e 2 x + e - x

Passo 1

Fala aí! Bora ver o que essa questão quer da gente?!

O enunciado nos da uma função f x = e 2 x + e - x   e pede algumas coisas em relação a ela:

  1. Os intervalos nos quais f é crescente ou decrescente.
  2. Os valores máximo e mínimos locais de f .
  3. Os intervalos de concavidade e os pontos de inflexão.

Pra isso a gente vai usar as derivadas primeira e segunda da função f ( x ) . Vamos nessa?!

Passo 2

Para encontrar onde f é crescente ou decrescente vamos calcular a primeira derivada de f :

f x = e 2 x + e - x

Vamos usar as regras de derivação da função exponencial, da cadeia e do polinômio:

e f x ' = e f x . f ' ( x )

F ' x = f ' g x . g ' x

x n ' = n x n - 1

Vamos agora aplicar:

f ' x = e 2 x . 2 x ' + e - x . - x '

f ' x = e 2 x . 2 x 1 - 1 + e - x . - x 1 - 1

f ' ( x ) = 2 e 2 x - e - x

Lembrando que: Se a derivada de uma função é positiva é sinal que ela é crescente, derivada negativa a função é decrescente!

Agora a gente precisa calcular a raíz da função pra depois fazermos o estudo de sinal:

2 e 2 x - e - x = 0

2 e 2 x = e - x

e 2 x e - x = 1 2

e 3 x = 1 2

Usando a definição de logaritmo podemos reescrever a igualdade:

3 x = ln ⁡ 1 2

x = 1 3 ln ⁡ 1 2

Agora sim, fazemos o estudo de sinal:

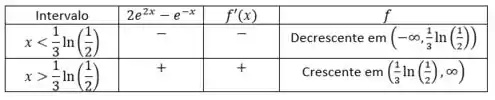
Passo 3

Para ser um ponto de máximo ou mínimo local, o sinal de f ' deve mudar nesse ponto. Já calculamos a raiz da função no passo anterior, então só precisamos analisar a tabela acima!

Vemos que em x = 1 3 ln ⁡ 1 2 há mudança do sinal de f ' , e como em x = 1 3 ln ⁡ 1 2 o sinal muda de negativo para positivo, então ele é um ponto de mínimo local.

Para achar os valores é só substituir os valores em f :

f 1 3 ln ⁡ 1 2 = e 2 1 3 ln ⁡ 1 2 + e - 1 3 ln ⁡ 1 2 = 1,89

Passo 4

Pra acabar queremos os intervalos de concavidade e os pontos de inflexão, para isso vamos calcular f ' ' ( x ) :

f ' ( x ) = 2 e 2 x - e - x

f ' ' x = 4 e 2 x + e - x

Os dois termos são sempre positivos, assim f é côncava para cima em - ∞ , ∞ e não há ponto de inflexão.

Resposta

  1. Crescente em 1 3 ln ⁡ 1 2 , ∞ e decrescente em - ∞ , 1 3 ln ⁡ 1 2
  2. f 1 3 ln ⁡ 1 2 = 1,89 é mínimo local
  3. Concavidade para cima em - ∞ , ∞ e não há ponto de inflexão
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem f x = e
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem f x = e
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem f x = x
Identifique os valores extremos locais das funções nos domínios dados informe onde eles ocorremQual dos valores extremos, se houver, é absolutoFundamente suas conclusões como uma calculadora ou progra
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem f x = x