Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.6 - Ex. 40
Encontre o limite ou demonstre que ele não existe:
Passo 1
Bom galera, pra esse problema a gente vai ter que fazer parte por parte e olhando o gráfico das funções, primeiro vamos separar:
A gente pode chamar o de , então vamos:
E esse vai ser o resultado do limite:
Passo 2
Beleza, a gente usar o gráfico da função logarítmica pra encontrar :
O gráfico é:
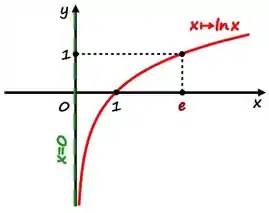
Assim, a gente vê que quando tende para pela direita ela vai caindo infinitamente para , logo:
Passo 3
Pronto, a gente pode aplica dentro daquele limite inicial, fica:
E a gente olha o gráfico da função inversa da tangente:
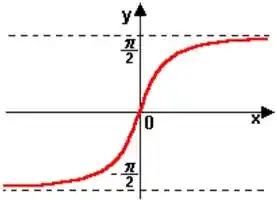
Assim a gente nota que quando tender para , a função vai se aproximar infinitamente de , então:
Resposta
Exercícios de Livros Relacionados
Modifique a definição para atender ao caso lim x → x 0 - f x = ∞
Utilize as definições formais para provar a afirmação lim x → - 5 1 x + 5 2 =∞
34. Prove o teorema 2.3.3
Esboce o gráfico da função e use-o para determinar os valores de a para os quais lim x → a f ( x ) existe. f x = 1 + s e nx s ex0 cos x s e0 ≤ x ≤ πs e nxs e xπ
Para a função f , cujo gráfico é dado, diga o valor de cada quantidade indicada, se ela existir. Se não existir, explique por quê .(a) lim x → 1 f x (b) lim x → 3 - f x (c) lim x → 3 + f x (d) l