Modifique a definição para atender ao caso

Da definição, já podemos concluir algo sobre a posição do . Lá temos que estamos à direita de ou seja, estamos com maiores um pouco que e, portanto,

Ou seja, estava na região pintada

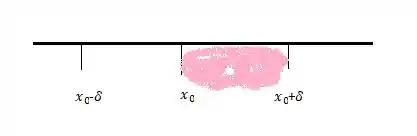
Como estamos á deireita de estamos trabalhando com a mesma região, então vamos manter essa parte da definição. Ou seja,

Além disso, do fato de que tende a temos que , roubando da definição de tender a , precisamos que .

Então tá feita essa bagaça.

Vamo colocar bonitinho agora:

Dizemos que se aproxima de quando se a próxima de pela direita e escrevemos se para todo existe um numero correspondente tal que para todo ,