Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 60

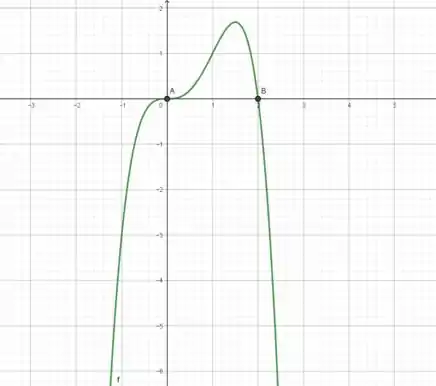
Encontre os limites quando e quando Use essa informação, bem como as intersecções com os eixos, para fazer um esboço do gráfico, como no Exemplo 12.

Passo 1

Olá, querido estudante. Vamos para mais uma resolução juntos.

Temos aqui a função

E iremos calcular o seu limite para quando

A partir dessas informações, e depois que encontrarmos também as intersecções com os eixos, que iremos fazer o esboço do gráfico. A questão cita que deveremos fazer como foi feito no Exemplo 12, que basicamente faz o que é pedido na questão, encontra as intersecções com os eixos, isto é

Após obtermos os pontos de intersecção e o limite da função, poderemos criar o gráfico da função, pois com esses dados já conseguiremos entender o comportamento da mesma.

Passo 2

Vamos então reescrever a função para que possamos analisar melhor:

Primeiro iremos analisar esse limite:

Olha só, imagina que você tem um número muito grande positivo elevado ao cubo (fica positivo) multiplicado por menos esse número grandão. Dentro do parêntese vai ficar negativo né? Tipo:

Então, nosso produto vai dar negativo e teremos que:

Ou seja, quanto mais o valor de cresce, mais a nossa função decresce.

Passo 3

Vamos ver o contrário agora:

Bom, aqui é o contrário né?! Vamos ter um número muito grande negativo elevado a , (que vai dar ) multiplicado por

Então vamos ter negativo multiplicado por positivo, o que nos leva a concluir que:

Isso é, quando estivermos caminhando para a esquerda no eixo , nossa função está caminhando para baixo no eixo .

Passo 4

Só falta as interseções com os eixos agora. Vamos lá:

Eixo : São as raízes da nossa função.

Então, a função intersecta o eixo em e

Eixo : Nossa função toca o eixo para

A interseção com então é no ponto

Passo 5

Juntando essas informações, a gente monta o gráfico no GeoGebra, para que ele fique mais bonito e você consegue entender melhor o resultado:

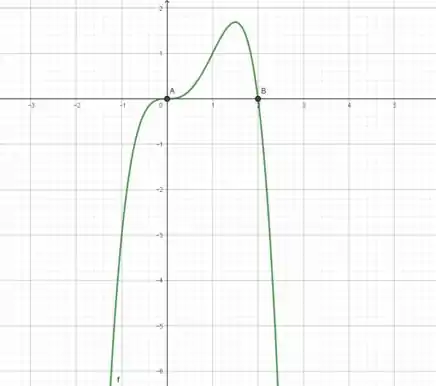
Aqui a gente consegue ver todos os pontos e comportamentos que a gente previu durantes nossos cálculos. Um forte abraço e até uma próxima meu amigo.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre as assindotas horizontal e vertical de cada curva. Se você tiver um dispositivo gráfico, confira pela curva gráfica as assindotas estimadas: y = 5 + 4 x x + 3

Encontre as assindotas horizontal e vertical de cada curva. Se você tiver um dispositivo gráfico, confira pela curva gráfica as assindotas estimadas: y = 2 x 2 + 1 3 x 2 + 2 x - 1

Encontre as assindotas horizontal e vertical de cada curva. Se você tiver um dispositivo gráfico, confira pela curva gráfica as assindotas estimadas: y = x 3 - x x 2 - 6 x + 5

Encontre as assíntotas horizontal e vertical de cada curva. Se você tiver um dispositivo gráfico, confira pela curva gráfica as assíntotas estimadas: y = 2 x 2 + x - 1 x 2 + x - 2

Encontre as assindotas horizontal e vertical de cada curva. Se você tiver um dispositivo gráfico, confira pela curva gráfica as assindotas estimadas: y = 1 + x 4 x 2 - x 4