Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.6 - Ex. 50
Encontre as assindotas horizontal e vertical de cada curva. Se você tiver um dispositivo gráfico, confira pela curva gráfica as assindotas estimadas:
Passo 1
Olá, meu amigo. Vamos partir para essa resolução.
A gente tem a função:
E precisamos encontrar as assíntotas horizontais e verticais dela. Antes de darmos inicio vamos dar uma revisada.
- Uma assíntota vertical ocorre quando a função se aproxima de um valor vertical específico à medida que a variável independente se aproxima de um determinado valor;
- As assíntotas verticais podem ocorrer devido a valores que fazem com que a função se torne indefinida, como divisões por zero ou raízes de denominadores polinomiais;
- Uma assíntota horizontal ocorre quando a função se aproxima de um valor horizontal específico à medida que a variável independente se aproxima de ou de ;
- Uma função pode ter uma assíntota horizontal em se a função se aproxima de à medida que se aproxima de
Bom galera, pra esse problema a gente deve saber que a assíntota horizontal pode ser dada por:
E a vertical, é o valor que quanto tender o função ir para o infinito:
Após todos esses cálculos, iremos plotar o gráfico da função com o auxílio do GeoGebra para que possamos ver se estamos certos nas nossas considerações.
Passo 2
Beleza, então, vamos começar calculando a assíntota horizontal:
Pra resolver esse limite, a gente põe o de maior potência em evidência, bem assim:
Agora a gente simplifica o :
Agora, a gente só aplica o limite, lembrando que quando um número é dividido por um número que tende ao infinito, ele tende a , então:
Nós encontramos assim:
Passo 3
Show de bola, vou te contar um macetinho sobre como calcular as assíntotas verticais, e depois explicar por que isso.
Pra encontrar essa assíntota a gente só precisa encontrar o valor de para quando o denominador (a parte debaixo da fração) for .
Agora, o porquê disso é bem simples, por que a assíntota não acontece quando o limite tende a infinito? Pois é, a função tende a infinito quando o denominador da função tende a , mas não é de fato zero, como as assíntotas, que são linhas que as nossas funções chegam perto, mas nunca tocam de fato.
Vamos usar isso agora, que vai ajudar a entender.
Passo 4
Pois é galera, vamos logo calcular essa assíntota vertical, bora pegar o limite:
Beleza, como eu disse no passo anterior, é só encontrar para que o denominador vai ser então:
Assim, resolvendo essa equação a gente acha:
Temos então:
Vamos testar no numerador pra ver se não causa indefinição do tipo
Como não deu tá tudo certo.
Passo 5
Vamos então agora ao gráfico:
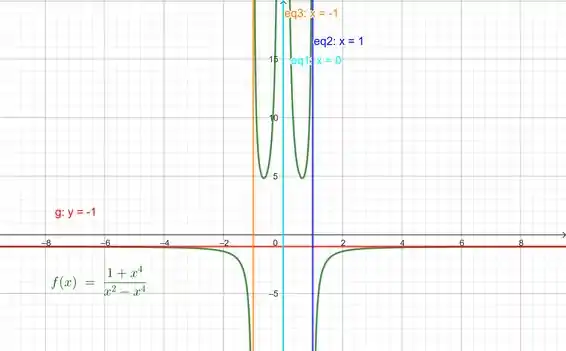
E é isso, resolvemos o nosso problema e estamos corretos, pelo gráfico acima.