Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 61
Encontre os limites quando e quando Use essa informação, bem como as intersecções com os eixos, para fazer um esboço do gráfico, como no Exemplo 12.
Passo 1
Bom, a primeira coisa que a gente pode fazer aí é fatorar pra ficar mais fácil. Temos que:
Beleza, agora a gente tem um produto de polinônimos.
O problema pede a interseção com os eixos e os limites com x tendendo a mais e menos infinito. Vamos fazer um por um...
Passo 2
Olha só, imagina que você tem um número muito grande elevado a (fica positivo) multiplicado por 1 menos esse número grandão ao quadrado.
Dentro do parêntese vai fica negativo né? Tipo: (só pra entender melhor)
Então, nosso produto vai dar negativo e teremos que:
Ou seja, quanto mais o valor de cresce, mais a nossa função decresce.
Passo 3
Vamos ver o contrário agora:
Bom, aqui é o contrário né?! Vamos ter um número muito pequeno elevado a 4, (que vai dar ) multiplicado por
Então vamos ter positivo multiplicado por negativo, o que nos leva a concluir que:
Quanto menor o , menor a função.
Passo 4
Só falta as interseções com os eixos agora. Vamos lá:
- Eixo
- Eixo
Então, a função intersecta o eixo em e
A interseção com então é no ponto
Passo 5
Juntando essas informações, a gente monta o gráfico:
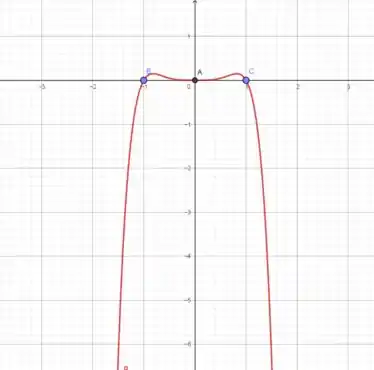
Resposta
Ei, a resposta está no passo a passo :)