Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 13.3 - Ex. 9
9. Encontre o ponto na curva 
unidades ao longo da curva a partir do ponto (0, 5, 0) na direção do comprimento de arco crescente.
Passo 1
Fala galerinha tranquilidade, nesse caso precisamos a partir do comprimento do arco encontrar o ponto, por definição o paramêtro de comprimento de arco é dado por:
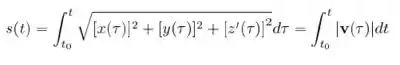
Considerando que não conhecemos o ponto t0, podemos encontrar ele seguindo os passos:
Passo 2
Para a velocidade que pode ser encontrada derivando a posição em relação ao tempo temos:
Passo 3
Como conhecemos o comprimento do arco:
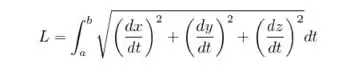
Podemos utilizar o valor já fornecido de L e ficar:
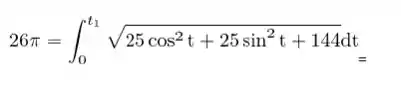
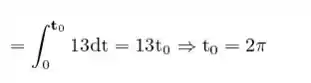
Resposta
O valor do ponto é:
Exercícios de Livros Relacionados
Mostre que para todo ponto da curva r → t = e t cos t , e t sin t , e t o ângulo entre o vetor tangente unitário e o eixo z é o mesmo. Em seguida, mostre que o mesmo resultado é válido para os vet
Encontre a equação do plano normal e do plano osculador para a curva dada pelo ponto. x = ln t ,y = 2 t , z = t 2 ; 0,2 , 1
Utilize um computador para traçar a curva da equação vetorial dada. Escolha o domínio do parâmetro e ponto de vista de forma a revelar a verdadeira natureza da curva. r t = t 4 - t 2 + 1 , t , t 2
Utilize um computador para traçar a curva da equação vetorial dada. Escolha o domínio do parâmetro e ponto de vista de forma a revelar a verdadeira natureza da curva. r t = t 2 , t - 1 , 5 - t
Utilize o computador para traçar a curva da equação vetorial dada. Escolha o domínio do parâmetro e ponto de vista de forma a garantir que a visualização é verdadeira. r → t =s e n t , c o s t , t 2