Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 13.3 - Ex. 3
Nos Exercícios 1-8, encontre o vetor tangente unitário da curva. Encontre também o comprimento da parte indicada da curva.
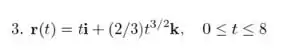
Passo 1
Fala galerinha tranquilidade, essa seção do livro pede para que nós calculemos o vetor tangente unitário, que seria o vetor dividido pelo módulo dele, utilizando a definição do livro:
Para o módulo da velocidade temos a raiz quadrada das componentes ao quadrado ficando:
Agora o vetor tangente unitário:
Passo 2
Para o segundo passo, precisamos encontrar o comprimento de arco que também seria a velocidade, também usando a definição do livro temos:
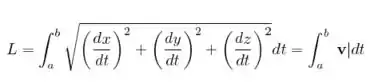
Utilizando a definição do passo dois, como já temos o módulo da velocidade, podemos integrar:
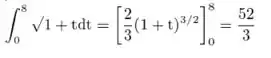
Resposta
Pronto bora para próxima. Vlw
Exercícios de Livros Relacionados
Encontre a curvature para r → t = t 2 , ln t , t ln t no ponto ( 1,0 , 0 ) .
Encontre o comprimento da curva para 4 casas decimais. (Use uma calculadora para aproximar a integral.) r → t = cos π t , 2 t , s e n 2 π t ,p a r a1,0 , 0a t é( 1,4 , 0 ) é
O plano retificante da curva e do ponto é o plano que contém os vetores T → e B → no ponto. Encontre o plano retificante da curva r → t = s e nti ^ + cos t j ^ + tan t k ^ E ao ponto 2 2 , 2 2 ,1
Encontre a equação do plano normal e do plano osculador para a curva dada pelo ponto. x = s e n 2 t ,y = - cos 2 t , z = 4 t ; ( 0,1 , 2 π )
Use o teorema 10 para encontrar a curvatura. r → t = t i ^ + t ² j ^ + e t k ^ ²