Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.Exercícios Práticos - Ex. 105
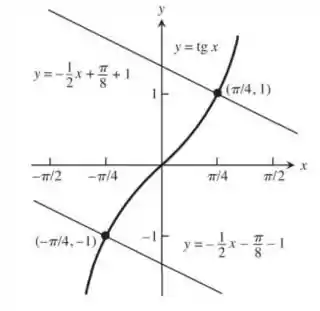
Encontre os pontos na curva , , em que a normal seja paralela à reta . Esboce a curva e as normais juntas, identificando cada uma com sua respectiva equação.
Passo 1
A primeira derivada de uma função em determinado ponto nos dá o coeficiente angular da reta tangente naquele ponto, portanto para resolver a questão precisaremos achar a primeira derivada da curva dada. Usaremos que o produto dos coeficientes angulares entre duas retas normais é igual a -1. Em seguida usaremos que os coeficientes angulares de duas retas paralelas é igual e que na equação da reta expressa o valor do coeficiente angular.
Passo 2
Agora usamos que os coeficientes angulares de duas retas paralelas são iguais e que na equação da reta expressa o valor do coeficiente angular.
Portanto:
Como , os valores de x são
Passo 3
Para determinar os valores de , substituímos os valores de obtidos na equação original:
Falta agora apenas esboçar o gráfico, usando e fazendo as retas cruzarem o gráfico nos pontos obtidos.
Resposta
