Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 25
Encontre as representações paramétricas das superfícies:
- A parte da esfera que está entre os planos e .
Passo 1
Fala, galera! Tudo tranquilo?
Essa questão quer a representação paramétrica da parte da esfera
que está entre os planos
e
Uma representação paramétrica de uma superfície são três funções e que dependem de dois parâmetros e essas funções dão as coordenadas , , de qualquer ponto na superfície.
Aqui no nosso caso temos que representar a parte da esfera que está entre os dois planos. Para parametrizar esferas, podemos usar o sistema de coordenadas esféricas
Retomando o significado de cada variável no espaço, temos o esquema:
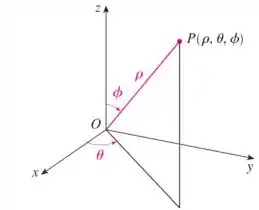
Então, vamos olhar nossa superfície e parametrizá-las em coordenadas esféricas.
Passo 2
E aí galerinha, vamos começar mais essa questão. A superfície que o enunciado descreve é:
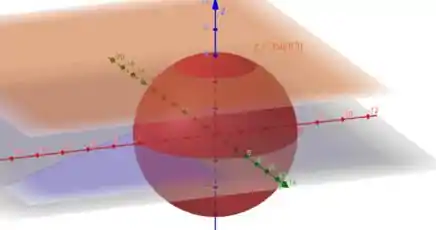
A primeira coisa que podemos fazer é parametrizar a esfera. A parametrização é dada por:
Como nossa equação da esfera é:
E sabemos que a equação~ o geral de uma esfera é:
Temos aqui que:
Então nosso raio é:
Substituindo nas equações, temos:
Passo 3
Mas nós não temos a esfera inteira, e sim a parte dela entre dois planos. Então nossas variáveis e vão ter um intervalo específico de domínio. Vamos achar esses valores: A interseção da esfera com o plano corresponde a:
Isolando:
Para isolarmos vamos aplicar sua função inversa, , nos dois lados da equação e ficamos com:
Agora, a interseção da esfera com o plano (o plano ) corresponde a:
Isolando:
Novamente aplicando , nos dois lados da equação e ficamos com:
Assim, a superfície é delimitada por
e a variável , como vemos na imagem, não tem nenhuma restrição, então sua variação é:
Resposta
A representação paramétrica é:
Com
e