Encontre as representações paramétricas das superfícies:

• A parte do cilindro que está acima do plano e entre os planos e .

Bom, o primeiro passo era escolher as coordenadas, lembra?

Como se trata de um cilíndrico e ele estão orientado ao longo do eixo y, a melhor escolha é utilizar as coordenadas cilíndricas , ou seja:

Vamos olhar a nossa equação :

Sabemos que a equação de um cilindro orientado dessa forma será:

Isso quer dizer então que o nosso raio será . Vamos reescrever as nossas coordenadas:

Vou plotar a representação gráfica para a gente visualizar melhor,ok?

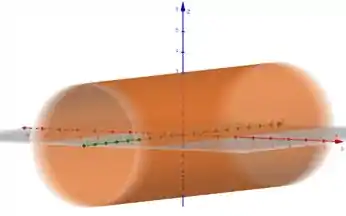
Lembrando que aqui ainda não colocamos a restrição, beleza?

Agora vamos para a nossa restrição. A primeira coisa que ele nos diz é que o cilindro precisa estar acima do eixo entre os planos . Isso quer dizer que .Se representarmos isso graficamente podemos entender melhor porque isso acontece.

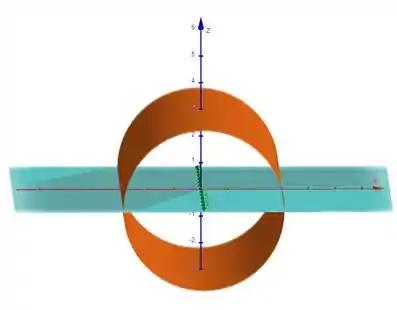
Bom, então se a nossa restrição é que seja sempre positivo , precisamos olhar para a nossa equação e nos perguntar para quais valores isso seria verdade.

Podemos ver que depende de , mais especificamente, do valor que será o . Então precisamos ver para qual região do círculo trigonométrico isso será verdade.

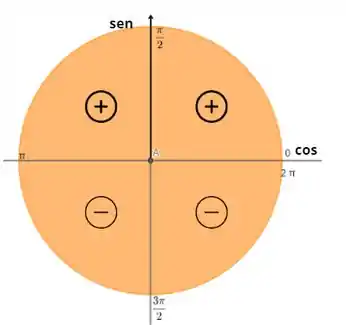
De acordo com o círculo trigonométrico, os valores para o seno de um ângulo ser positivo será quando :

Logo, essa será a nossa restrição.

Como ele também pede que o cilindro esteja entre os planos e e nós não mudamos o valor de , essa restrição vai se manter igual.