Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 30
Encontre as equações paramétricas da superfície obtida pela rotação da curva , ao redor do eixo e use-as para traçar o gráfico da superfície.
Passo 1
E aí, galerinha! Tudo certo?
Galera, antes de discutirmos os problemas, vamos pensar no que acontece quando rotacionamos um ponto ao redor do eixo . Nós teremos uma circunferência num plano paralelo ao plano de raio , uma vez que é a distância do ponto ao eixo . Nós podemos parametrizar essa equação da circunferência como .
Agora, considere uma curva no plano dada por . Quando rotacionada ao redor do eixo , temos uma superfície que é uma junção de circunferências com a seguinte representação paramétrica
Então, de acordo com o que achamos acima, vamos escrever nossos parâmetros como:
Onde o enunciado nos deu que:
Daí é só jogarmos nossas equações paramétricas e as restrições para em um software gráfico como o GeoGebra e obter nossa superfície.
Passo 2
Agora, quando nossa curva é rotacionada ao redor do eixo , nós temos a superfície que a representação paramétrica é dada por:
E, fazendo a substituição:
Também temos:
E:
Aqui vemos que nossas funções paramétricas dependem de dois parâmetros, cuja variação é:
- Para : como o próprio enunciado nos deu:
- Para : como não temos restrições para essa variável, ela pode assumir qualquer valor de ângulo:
1
E:
Passo 3
Usando um programa para traçar o gráfico, temos:
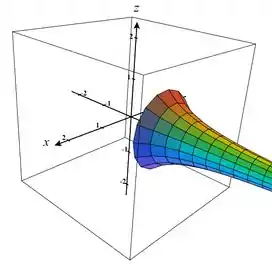
Resposta
A representação paramétrica é:
Com e .