Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 3.1 - Ex. 19
Encontre a solução do problema de valor inicial.
Faça o gráfico dasolução para e determine seu valor mínimo
Passo 1
Para resolvermos esse problema iremos analisar cada tipo de EDO e escolher o melhor método para resolvermos a mesma. Após isso, vamos aplicar esse método nos atentando com os casos complicados que podem aparecer. Para o problema de valor inicial, usaremos uma relação dada no capítulo para as constantes, onde resolvemos um sistema e chegamos que
Vamos resolver juntos!!
Passo 2
Bom, como para esse capítulo vamos apenas cair no caso onde a nossa equação característica é dada por , temos que haverá duas soluções para nossa equação. Supondo então que nossa solução é dada por , temos que nossa solução geral será
e
Ficando com e . Substituindo em nossa EDO, temos que
Caimos em uma equação de segundo grau. Resolvendo pelo método de Bhaskara, chegamos que
Tendo como raízes e . Assim, temos que nossa solução geral para a EDO dada é
Passo 3
Aplicando as condições de contorno, temos que nossas constantes serão dadas pela relação mostrada no Passo 1, assim temos que
Assim nossa equação que satisfaz a EDO é
E o gráfico é algo desse tipo
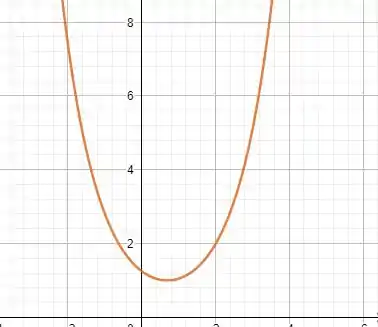
Para encontrarmos o ponto de mínimo, precisamos derivar a equação encontrada e igualar a 0. Fazendo isso, temos que sua derivada será
Aplicando o logaritmo natural, ficamos com
Sendo esse nosso ponto de mínimo.