Uma partícula de massa desloca-se sobre o eixo sob a ação da força elástica e de uma força de amortecimento proporcional à velocidade dada por determine a posição da partícula no instante t e discuta o movimento, supondo

Imagine que temos uma bancada ou uma mesa, e que a largura da mesa é o eixo, em cima dessa mesa temos uma partícula que está sofrendo uma força elástica e uma força de amortecimento proporcional a velocidade.

Vamos entender o que tudo isso quer dizer:

A velocidade é sendo que nosso espaço é o quanto a partícula desloca no eixo , ou seja:

Essa força de amortecimento é proporcional à velocidade, ou seja, tem um coeficiente de proporcionalidade que multiplica a velocidade e temos essa força de amortecimento. No caso dado é , assim temos que a (o quer dizer que ele está no sentido contrário ao eixo ).

A força elástica é dada por:

Para esse caso por isso temos: (o quer dizer que ele está no sentido contrário ao eixo ).

Sabemos que o somatório de forças em é igual a

Sendo que o exercício diz que e sabemos que que, como já vimos acima, como ela se desloca sobre o eixo teremos:

Assim:

Passo 2

Agora que sabemos qual a relação com as forças vamos tentar achar a relação

Se usarmos, para esse caso que , assim:

Identificados os valores de, podemos Agora reescrever o pelo teorema que diz que se temos duas raízes da equação característica (ou seja, a função ), então se podemos afirmar que:

Assim, substituindo os valores de :

Nesse caso, precisamos também de para aplicar o:

Passo 3

1. Agora que achamos essas duas relações podemos substituir os valores:

Assim:

Precisamos entender o comportamento dessa função.

Sabemos que a derivada dela é:

Ele limita assim, para função dada vamos ver o seguinte:

• A função é sempre negativa no intervalo , ou seja, a função é sempre decrescente;
• Como t cresce mais devagar que podemos afirmar que no intervalo dado a derivada decresce, ou seja, diminui mais devagar.
• O , ou seja, a função tende pra 0 conforme se aproxima de .

Assim espera-se que o gráfico seja algo assim:



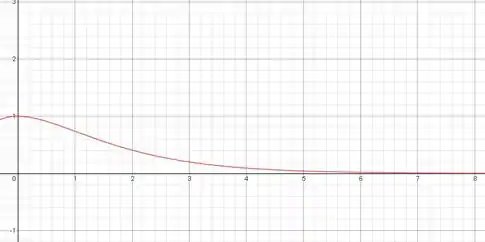
A interpretação pro caso dado é que se equivale ao espaço percorrido, e o tempo decorrido conforme o experimento.

Vemos que o é máximo no começo do experimento, enquanto ele tende a 0 conforme o tempo passa, isso pode ser entendido como efeito do amortecimento e da força elástica aplicada ao corpo

Passo 4

• O mesmo para o outro caso:

Precisamos entender o comportamento dessa função.

Sabemos que a derivada dela é:

Ele limita assim, para função dada vamos ver o seguinte:

• A função é sempre negativa no intervalo , ou seja, a função é sempre decrescente;
• é decrescente.
• O , ou seja, a função tende pra 0 conforme se aproxima de .

Assim espera-se que o gráfico seja algo assim:

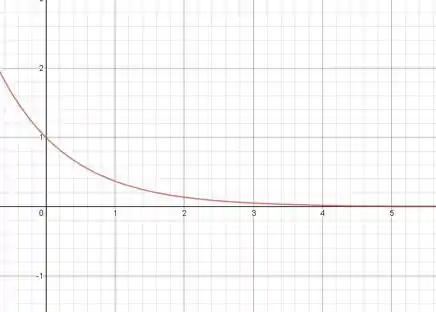
A interpretação pro caso dado é que se equivale ao espaço percorrido, e o tempo decorrido conforme o experimento.

Vemos que o é máximo no começo do experimento, enquanto ele tende a 0 conforme o tempo passa, isso pode ser entendido como efeito do amortecimento e da força elástica aplicada ao corpo

Vemos que ele decresce mais rápido pra esse caso,