Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 39

Encontre todos os pontos de interseção das curvas dadas

r = 1

r = 2 sen ⁡ 2 θ

Passo 1

Fala pessoal. De boa por ai?

Vamos resolver uma questão sobre pontos de interserção. Vamos fazer uma leitura do enunciado e pensar em como podemos resolver? Simbora!

O objetivo desta questão é encontrar todos os pontos de interseção das curvas dadas pelas equações polares, r = 1 e r = 2 sen ⁡ 2 θ . Essas curvas podem se cruzar em múltiplos pontos, e a solução envolve identificar todos esses pontos.

Se liga nos passos que preparei para resolvermos.

  1. Igualar as equações
  2. Isolar o termo trigonométrico para encontrar o valor de θ
  3. Considerar o intervalo e substituir os ângulos nas equações.

É isso pessoal, não tem segredo!

Passo 2

Para encontrar o ponto de interseção, igualamos as duas expressões para r , temos

r = 1

r = 2 sen ⁡ 2 θ

Então

1 = 2   s e n   2 θ

Isolando s e n   2 θ

s e n   2 θ = 1 2

Passo 3

Sabemos as equações, agora temos que verificar os ângulos. Para isso, porque não pedirmos uma ajudinha a um recurso gráfico para vermos a cara na nossa curva?

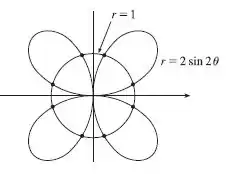
Aqui está!

Na imagem acima, marquei os pontos de interseção, temos então que encontrar ao todo, 8 pontos. Vamos encontra-los.

Passo 4

Vamos encontrar valores de θ . Sabemos que s e n   2 θ = 1 2 tem múltiplas soluções dentro do intervalo 0 ≤ 2 θ ≤ 2 π . Vamos encontrar os valores de 2 θ primeiro.

On ângulos no primeiro quadrante

2 θ = π 6 + 2 k π  

Ou

2 θ = π - π 6 + 2 k π

Simplificando

2 θ = 5 π 6 + 2 k π

Dividindo por 2 as duas equações para θ .

θ = π 12 + k π

Outro ângulo será

θ = 5 π 12 + k π

Onde k ∈ Z

Passo 5

Vamos agora considerar o intervalo 0 ≤ θ ≤ 2 π

Considerando todas as possíveis soluções dentro do intervalo.

Para k = 0

θ = π 12 + 0 ∙ π = π 12

Outro ângulo será

θ = 5 π 12 + 0 ∙ π = 5 π 12

Para k = 1

θ = π 12 + 1 ∙ π = 13 π 12

Outro ângulo será

θ = 5 π 12 + 1 ∙ π = 17 π 12

Sendo assim, os ângulos θ no intervalo de 0 ≤ 0 < 2 π , com r   = 1

θ = π 12 , 5 π 12 , 13 π 12 , 17 π 12

Passo 6

Precisamos agora considerar os valores de r > 0 , é importante lembrar que as coordenadas polares permitem que o valor de r seja negativo, o que corresponderá a um ponto so sentido oposto do ângulo θ . Vamos resolver a equação para r = - 1 e verificar quais sâo os ângulos correspondentes.

Para r = - 1

- 1 = 2   s e n   2 θ

Isolando s e n   2 θ

s e n   2 θ = - 1 2

Vamos agora encontrar valores de θ para essa situação.

Passo 7

Sabemos que s e n   2 θ = - 1 2 tem múltiplas soluções dentro do intervalo 0 ≤ 2 θ ≤ 2 π . Vamos encontrar os valores de 2 θ primeiro.

2 θ = - π 6 + 2 k π  

Simplificando

θ = - π 12 + k π

Outro ângulo será

2 θ = π + π 6 + 2 k π

Simplificando

2 θ = 7 π 6 + 2 k π

Dividindo ambos os θ por 2

θ = 7 π 12 + k π

Onde k ∈ z

Passo 8

Vamos agora considerar o intervalo 0 ≤ θ ≤ 2 π

Considerando todas as possíveis soluções dentro do intervalo.

Para k = 0

θ = - π 12 + 0 ∙ π = - π 12

Equivalente a

θ = 2 π - π 12 = 23 π 12

e

θ = 7 π 12 + 0 ∙ π = 7 π 12

Para k = 1

θ = - π 12 + 1 ∙ π = 11 π 12

E

θ = 7 π 12 + 1 ∙ π = 19 π 12

Sendo assim, os ângulos θ no intervalo de 0 ≤ 0 < 2 π , com r   = - 1

θ = 7 π 12 , 11 π 12 , 19 π 12 , 23 π 12

Passo 9

O que acha de observarmos esses ângulos na nossa curva?

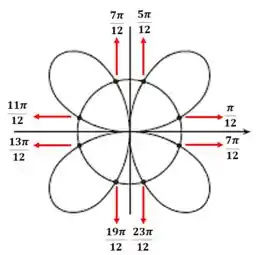
Resposta

Para r = 1 ,   θ pode valer:

θ = π 12 , 5 π 12 , 13 π 12 , 17 π 12

E para r = - 1 , θ pode valer:

θ = 7 π 12 , 11 π 12 , 19 π 12 , 23 π 12

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre todos os pontos de interseção das curvas dadas r = sen ⁡ θ r = sen ⁡ 2 θ
Encontre todos os pontos de interseção das curvas dadas r = 1 + sen ⁡ θ r = 3 sen ⁡ θ
Encontre todos os pontos de interseção das curvas dadas r = cos ⁡ 3 θ r = sen ⁡ 3 θ
Encontre todos os pontos de interseção das curvas dadas r = 1 - cos ⁡ θ r = 1 + sen ⁡ θ