Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 40
Encontre todos os pontos de interseção das curvas dadas
Passo 1
Fala pessoal. De boa por ai?
Vamos resolver uma questão sobre pontos de interserção. Vamos fazer uma leitura do enunciado e pensar em como podemos resolver? Simbora!
O objetivo desta questão é encontrar todos os pontos de interseção das curvas dadas pelas equações polares, e . Essas curvas podem se cruzar em múltiplos pontos, e a solução envolve identificar todos esses pontos.
Se liga nos passos que preparei para resolvermos.
- Igualar as equações
- Isolar o termo trigonométrico para encontrar o valor de
- Considerar o intervalo e substituir os ângulos nas equações.
É isso pessoal, não tem segredo!
Passo 2
Para encontrar o ponto de interseção, igualamos as duas expressões para , temos
Então
Dividindo ambos onlados por
Passo 3
Temos a equação polar, agora temos que verificar os ângulos. Para isso, porque não pedirmos uma ajudinha a um recurso gráfico para vermos a cara na nossa curva?
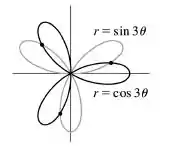
Pela figura, podemos perceber que existem três pontos de interseção entre as duas curvas. Vamos buscar esses pontos.
Passo 4
Igualando as curvas:
Assim
Ou
E com isso, só encontramos dois pontos.
Mas aí, se você reparar, esses dois valores de que achamos estão no primeiro e terceiro quadrante.
Acontece que, pela figura, temos um ponto de interseção que ocorre no segundo quadrante. E mais: bem no meio do segundo quadrante. Assim, podemos dizer que o nosso terceiro que tá faltando é
(ou você podia considerar também e teríamos para tangente igual a 1:
Belezinha?
Passo 5
Agora que já encontramos os valores de para os quais as duas curvas se intersectam, vamos encontrar o valor de também?
Assim a gente forma o ponto bonitinho e fecha logo a questão!
Para isso, é só substituir os valores de em uma das curvas, já que como é um ponto de inteseção, tanto faz a curva que vamos escolher, as duas vão dar o mesmo ponto!
Para :
Para :
Para :
Os pontos de interseção são portanto: