Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 49
Trace a curva com uma ferramenta gráfica e calcule seu comprimento
Passo 1
Olá, meu amigo. A gente vai traçar a curva da função:
Que é uma função parametrizada.
Iremos traçar essa curva com o auxílio do GeoGebra, além disso, vamos também calcular o comprimento da curva.
O comprimento de uma curva em coordenadas polares é dado por
Onde é o intervalo que queremos calcular o comprimento da curva.
Passo 2
Vamos começar traçando a curva, até mesmo pra gente poder descobrir o intervalo de variação do , e consequentemente o .
Se fizermos teremos:
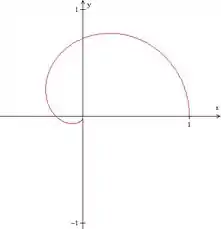
Que tem mó cara de ser uma curva pela metade né? Hahaha
Então vamos traçar essa curva de até , que aí sim teremos uma curva completa!
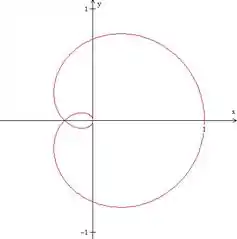
Passo 3
Agora vamos calcular o comprimento.
O comprimento de uma curva em coordenadas polares é dado por
O intervalo de integração a gente descobriu ali no passo 1:
Os outros termos da integral vão ficar:
Derivando a equação de , precisamos utilizar a regra da cadeia:
Agora elevando ao quadrado:
Passo 4
Substituindo tudo na integral:
Vamos colocar em evidencia o termo do cosseno elevado a 6ª pois assim conseguiremos utilizar de uma identidade trigonométrica:
Reescrevendo:
Retirando da raiz:
A gente pode reescrever dessa forma:
Utilizando da identidade trigonométrica:
Vamos dividir para conquistar:
Com uma substituição simples resolvemos:
E assim:
O gráfico do primeiro é positivo em todo o seu comprimento, mas o segundo é positivo até , negativo até , exatamente cancelando a primeira metade. Podemos corrigir isso alterando os limites para a e dobrando-os.
Calculando com o intervalo de integração:
Temos então: