Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.4 - Ex. 38
Encontre todos os pontos de interseção das curvas dadas
Passo 1
Olá, meu querido estudante. Vou te ajudar a resolver essa atividade.
Aqui a gente tem as duas curvas parametrizadas:
Quer dizer então que precisamos encontrar os pontos de interseção das duas curvas. Para isso, basta igualarmos as duas curvas.
Veja que com isso iremos encontrar os valores de onde as curvas se encontram, depois é só a gente pegar esses valores e substituir em qualquer uma das equações para a gente descobrir então os valores de quando isso ocorre.
Um outro ponto que deveremos testar é se ocorre das curvas se encontrarem na origem, isso é . Esse ponto não vai, necessariamente, aparecer igualando as curvas. Precisamos sempre testar ele separadamente. A maneira de testar é checando se as duas funções têm para algum valor de . Qualquer valor. Não precisa ser o mesmo valor para o dois. Se isso acontecer, as funções se encontram na origem.
Passo 2
Quer dizer então que precisamos encontrar os pontos de interseção das duas curvas.
Para isso, basta igualarmos as duas curvas:
Logo,
Ou
Agora vamos testar se elas se encontram na origem:
Agora para:
Sendo assim, eles se encontram na origem.
Passo 3
Agora que já encontramos os valores de para os quais as duas curvas se intersectam, vamos encontrar o valor de também?
Assim a gente forma o ponto bonitinho e fecha logo a questão!
Para isso, é só substituir os valores de em uma das curvas, já que como é um ponto de inteseção, tanto faz a curva que vamos escolher, as duas vão dar o mesmo ponto!
Para :
Para :
Os pontos de interseção são, portanto,:
E
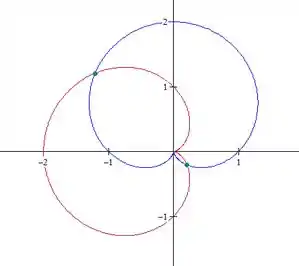
Vou desenhar a curva aqui com os pontos de interseção só para você visualizar melhor, mas não precisava disso, ok?
