Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.7 - Ex. 20
O deslocamento (em metros) de uma partícula movendo-se ao longo da reta é dado pela equação , onde é medido em segundos.
Encontre as velocidades médias sobre os seguintes intervalos de tempo:
Encontre a velocidade instantânea quando .
Faça o gráfico de como função de e desenhe as retas secantes cujas inclinações sejam as velocidades médias da parte , e a reta tangente cuja inclinação seja a velocidade instantânea da parte .
Passo 1
Fala aí, belezinha?
Bom, essa questão dá pra gente uma função de deslocamento de uma partícula ao longo do tempo, expressa por:
E pede para que a gente analise algumas coisas sobre esse movimento.
Vamos dividir cada um dos itens pedidos em passos para entender melhor o que fazer.
Vem que te ajudo com isso.
Passo 2
O item a) pede para que encontremos a velocidade média em cada um dos intervalos dado.
A velocidade média pode ser calculada fazendo:
Assim, precisaremos saber as posições do móvel em cada instante dado, e então poderemos aplicar essa fórmula aí para cada um dos casos.
Organizarei os espaços por instante de tempos!
Para
Para
Para
Para
Para
Agora que já temos todas as posições que precisamos, basta calcular a velocidade média para cada intervalo. Assim:
Calculando a velocidade de :
Calculando a velocidade de :
Calculando a velocidade de :
Calculando a velocidade de :
E prontinho. Letra a) resolvida.
Passo 3
O item b) pede pra gente calcular a velocidade instantânea pata .
Bom, a velocidade instantânea é dada por:
Então, vamos calcular a velocidade instantânea no instante fazendo
E lembrando que já calculado anteriormente.
Colocando tudo na expressão do limite, temos:
E foi, velocidade instantânea igual a zero para .
Passo 4
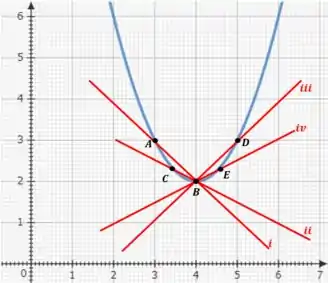
O item pede pra gente fazer o gráfico de como função de e desenhe as retas secantes cujas inclinações sejam as velocidades médias da parte , e a reta tangente cuja inclinação seja a velocidade instantânea da parte .
Bom, para isso precisaremos do gráfico de , que é uma parábola com concavidade voltada para cima, dada por:
Do item a) teremos:
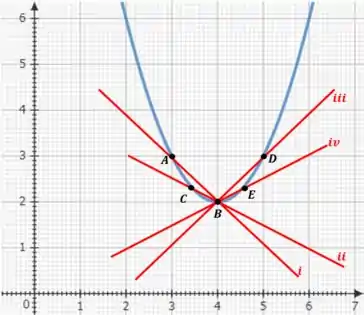
A reta tem inclinação igual velocidade média )
A reta tem inclinação igual velocidade média )
A reta tem inclinação igual velocidade média )
A reta tem inclinação igual velocidade média )
E do item b) teremos:
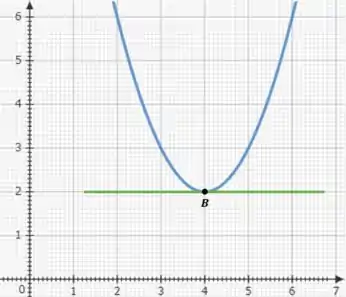
A reta que passa pelo ponto tem inclinação zero, que a igual a velocidade instantânea no ponto
Resposta
)
