Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.6 - Ex. 64
Encontre o valor exato de cada expressão
Passo 1
Olá, meu caro colega. Vamos para mais uma resolução?
Desejamos encontrar o valor exato da expressão dada em cada alternativa. Estamos trabalhando aqui com as funções trigonométricas inversas.
Assim, devemos lembrar que para as funções inversas o raciocínio deve ser o inverso do que fazemos com a função normal, ou seja, devemos pensar qual é o arco cuja função da o resultado entre parênteses.
Passo 2
Então, a gente tem que pensar em qual ângulo encontramos o valor da tangente de ? Podemos ver isso no círculo trigonométrico completo:
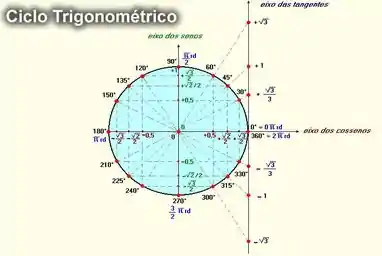
Veja então que o ângulo de é o ângulo que buscamos:
Isso nos indica que o arco cuja tangente tem valor igual a é o arco de .
Passo 3
Para a segunda alternativa iremos utilizar o mesmo raciocínio, mas lembrar que:
Então:
Analisando então o círculo trigonométrico, precisamos do arco que nos de o , pois o é o seu inverso.
Ou seja, o arco (ângulo) cuja cossecante dá é o arco de