Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.6 - Ex. 6
Uma função f é dada por um gráfico. Determine se f é injetora.
Passo 1
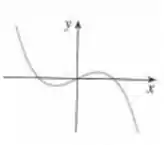
Opa, bora lá! O enunciado nos dá o seguinte gráfico:
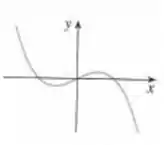
E pede pra a gente dizer se a função é injetora.
Bom, para saber se uma função é injetora, vamos ver o conceito de função injetora. Uma função injetora é uma função que para cada valor no contradomínio existe apenas um valor no domínio associado. Veja no exemplo:
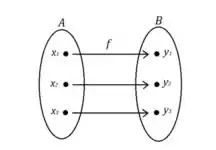
A é o domínio e B é o contradomínio
Passo 2
Agora, vamos ver como o gráfico se comporta:
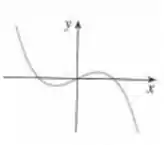
Repare no eixo (, o gráfico intercepta ele em mais de um ponto. Isso significa que existe um valor do contradomínio que é associado a mais de um valor no domínio. Assim, a função não é injetora.
Prontinho!
Resposta
A função f não é injetora.
Exercícios de Livros Relacionados
Uma função f é dada por um gráfico. Determine se f é injetora.
(a) O que é uma função injetora?(b) A partir do gráfico, como dizer se uma função é injetora?
Se for dado o gráfico de f , como você encontrará o gráfico de f - 1 ?
(b) Se for dada uma fórmula para f , como você encontrará uma fórmula para f - 1 ?
Uma função f é dada por uma tabela de valores. Determine se f é injetora.