Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 1
(a) O que é uma função injetora?
(b) A partir do gráfico, como dizer se uma função é injetora?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente definir uma função injetora e dizer como identificar uma função injetora a partir do gráfico.
Então, vamos lembrar lá da teoria a relação entre domínio e contradomínio de uma função, para definir o que é uma função injetora e relembrar como se comporta o gráfico dessa função.
Vamos lá!
Passo 2
Bom, uma função injetora é aquela em que a função passa somente uma vez por um valor do contradomínio (). Isto é, se pegarmos quaisquer valores do domínio, como , podemos ter a certeza de que .
Pensando que é o domínio e é o contradomínio, esse é o diagrama de uma função injetora:
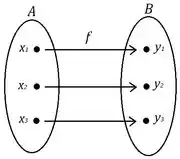
Passo 3
Agora para sabermos se uma função é injetora, temos o teste da reta horizontal. Esse teste nos diz que uma função é injetora se nenhuma reta horizontal intercepta seu gráfico em mais de um ponto.
Então, temos que imaginar linhas horizontais no gráfico e testar se alguma dessas linhas intercepta o gráfico mais de uma vez. Se isso ocorrer, é porque um único valor de está associado a mais de um valor de , então a função não pode ser injetora, certo?
Valeu, galera! Até a próxima! 😉
Resposta
(a) Função injetora: existe apenas um valor de associado a um valor de .
(b) Uma função é injetora se nenhuma reta horizontal intercepta seu gráfico em mais de um ponto.