Um homem começa a andar para o norte a 4 pés/s a partir de um ponto P. Cinco minutos depois uma mulher começa a andar para o sul a 5 pés/s de um ponto a 500 pés a leste de P. A que taxa as pessoas est��o se separando 15 minutos depois de a mulher começar a andar?
Passo 1
Opa, bora lá! Vamos analisar o que nosso probleminha está falando.
Vamos fazer um esqueminha para a gente entender o que est�� acontecendo.
Bom, ele nos diz que tem duas pessoas, um carinha que sai andando para o norte a partir de um ponto P, e uma mulher que anda para o sul a partir de um ponto a 500 pés a direita (leste) de P, 5 minutos depois que o homem já estava andando.
Até então o que temos é isso daqui.
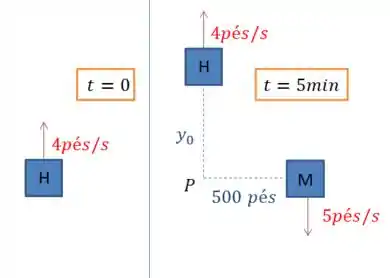
Ele nos pede a variação da distância entre eles 15 minutos depois da moça começar a caminhar.
Beleza, a partir do instante que a moça começa a andar até 15 minutos depois, o que temos é isso aqui:
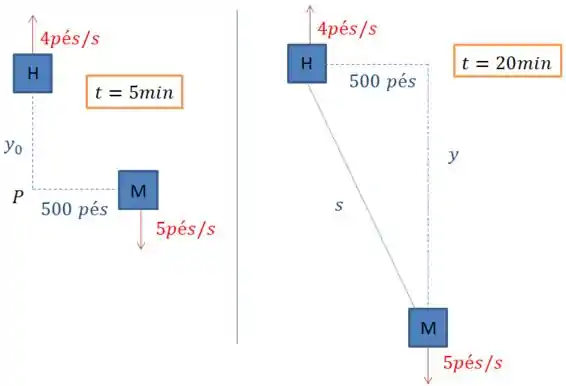
Repara que a gente acaba formando um triângulozão ali na direita.
Vamos utilizar Pitágoras para encontrar o que queremos, lembrando que aqui queremos encontrar a taxa de variação da distância entre eles minutos depois da moça começar a andar.
Portanto, queremos encontrar:
E podemos encontrar fazendo Pitágoras:
Vamos lá então?
Passo 2
Fazendo Pitágoras, temos que:
Derivando ambos os lados com relação ao tempo, temos:
Aqui, precisamos saber qual a taxa de variação de .
Você concorda que podemos ver como sendo a soma distância que o homem percorre com a distância que a moça percorre , dessa forma:
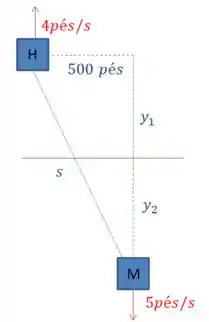
Portanto, podemos falar que:
E se queremos encontrar , podemos fazer:
Ou seja, a variação do do triângulo é a soma das variações em e , o que faz sentido né.
Passo 3
Voltando para a nossa expressão, temos:
Resolvendo para e substituindo o que encontramos:
Agora, nos resta encontrar a altura total e a distância entre eles, no instante de tempo pedido.
Bom, sabemos que o homem está se locomovendo para cima já há minutos (1200 segundos), portanto, é igual a:
E a moça está se locomovendo para baixo já há 15 minutos (900 segundos), portanto, é igual a:
Dessa forma, a altura total do triângulo é:
Passo 4
Agora nos resta encontrar a distância total entre eles nesse instante de tempo dado.
Para isso, podemos voltar para o Pitágoras que aplicamos no triângulo grande.
Substituindo a altura que encontramos:
Agora basta substituirmos na expressão a seguir para encontrar .
E prontinho, conseguimos entregar essa!